| Autor |
Beitrag |
    
Kilian (Quaternion)

| | Veröffentlicht am Dienstag, den 16. Januar, 2001 - 22:56: | 
|
ich suche nach einer anregung zu einem beweis der tatsache dass die 26 die einzige Zahl ist,
die zwischen einer kubik und einer quadratzahl liegt, oder äquivalent alle natürlichen zahlenpaare (a,b), die die Gleichung:
a³-b²=2 erfüllen.
Dies können eigentlich nur 3 und 5 sein, habe aber keine konstruktive idee. Habe es schon mit diversen teilbarkeitssätzen probiert und versucht mit den Abständen von a und b selber zu operieren. Zwar ist es leicht zu beweisen, dass z.b. a!=b sein muss und a-b=2 automatisch auf (3,5) schliesst. Allerdings habe ich keine induktion zusammengebracht, da die gleichungen zu komplex sind. vielleicht gibt es ja eine andere idee. |
    
SpockGeiger (Spockgeiger)

| | Veröffentlicht am Dienstag, den 23. Januar, 2001 - 19:19: | 
|
Hi Kilian
Ich wollte Dich wissen lassen, dass Deine Nachricht nicht auf taube Ohren
gestoßen ist, auch wenn mir leider bisher u.a. wegen Zeitmangel wenig
Konstruktives dazu eingefallen ist. Kannst Du bitte ausführlicher darlegen,
was Dir bisher dazu eingefallen ist? Vor allem die Induktion würde mich
interessieren, weil ich noch nicht mal ne Idee hätte, wie man da mit
Induktion rangehen sollte.
viele Grüße
SpockGeiger |
    
Matroid (Matroid)

| | Veröffentlicht am Freitag, den 26. Januar, 2001 - 19:38: | 
|
Mich interessiert die Aufgabe auch.
Ich hab's mal mit Modulo-Arithmetik versucht und bekomme damit auch einige passende Teilergebnisse.
Etwa so:
Wenn a³-b²=2, dann gilt auch a³-b² mod2 = 0
=> beide gerade oder beide ungerade
Wenn a³-b²=2, dann gilt auch a³-b² mod3 = 2
| | | a mod 3 | b mod 3 | a³ mod 3 | 2*b² mod 3 | a³-b² mod 3 | | 0 | 0 | 0 | 0 | 0 | | 0 | 1 | 0 | 2 | 2 | | 0 | 2 | 0 | 2 | 2 | | 1 | 0 | 1 | 0 | 1 | | 1 | 1 | 1 | 2 | 0 | | 1 | 2 | 1 | 2 | 0 | | 2 | 0 | 2 | 0 | 2 | | 2 | 1 | 2 | 2 | 1 | | 2 | 2 | 2 | 2 | 1 | | | |
=>
beide gerade oder beide ungerade
Mit mod4 findet man noch:a mod3=0 und (b mod3=1 oder b mod3=2)
a mod3=2 und b mod3=0
=> eine von beiden durch 3 teilbar
Mit mod5:
a mod5 != 0 und a mod5 != 4
d.h. weder a noch a+1 ist durch 5 teilbar
Aber so ganz allgemein findet ich keine Idee.
Gruß
Matroid
usw. |
    
Zaph (Zaph)

| | Veröffentlicht am Samstag, den 27. Januar, 2001 - 13:54: | 
|
Nicht ganz das, was ihr sucht:
a = 129/100, b = 383/1000. |
    
Matroid (Matroid)

| | Veröffentlicht am Samstag, den 27. Januar, 2001 - 16:40: | 
|
Hi Zaph, auf welchem Weg hast Du diese Lösung
gefunden? |
    
Zaph (Zaph)

| | Veröffentlicht am Samstag, den 27. Januar, 2001 - 19:12: | 
|
Wenn (a,b) eine Lösung ist, dann auch immer (c,d) mit
c = m² - 2a
d = b + m(c - a)
wobei
m = 3a²/2b
*g* |
    
Zaph (Zaph)

| | Veröffentlicht am Montag, den 29. Januar, 2001 - 20:45: | 
|
Hoffentlich liest sich das jemand durch, denn es war viel Arbeit, das einzuscannen :-/
In der Einleitung des Buchs "Rational Points on Elliptic Curves" von Joseph H. Silverman und John Tate (Springer-Verlag 1992) habe ich zufällig das Folgende gefunden. (Schreibfehler stammen durch Scanfehler oder durch falsches Abtippen. Ich hoffe, die meisten sind raus.)
The theory of Diophantine equations is that branch of number theory which deals with the solution of polynomial equations in either integers or rational numbers. The subject itself is named after one of thc greatest of the ancient Greek algebraists, Diophantus of Alexandria, who formulated and solved many such problems.
Fußnote: Diophantus lived sometime before the 3rd century A. D. He wrote the Arithmetica, a treatise on algebra and number theory in 13 volumes, of which 6 volumes have survived.
Most readers will undoubtedly be familiar with Fermat's Last Theorem.
Fußnote: Fermat's Last "Theorem" is really a conjecture, because it is still unsolved after more than 350 years. Fermat stated his "Theorem" as a marginal note in his copy of Diophantus' Arithmetica; unfortunately, the margin was too small for him to write down bis proof!
Anmerkung: Das Buch ist von 1992!
This theorem says that if n > 3 is an integer, then the equation
Xn + Yn = Zn
has no solutions in non-zero integers X, Y, Z. Equivalently, the only solutions in rational numbers to the equation
xn + yn = 1
are those with either x = 0 or y = 0. Fermat's Theorem is now known to be true for all exponents n <= 125000, so it is unlikely that anyone will find a counterexample by random guessing. On the other hand, there are still a lot of possible exponents left to check between 125000 and infinity!
As another example, wo consider the problem of writing an integer as the difference of a square and a cube. In other words, we fix an integer c and look for solutions to the Diophantine equation
y2 - x3 = c.
Fußnote: This equation is often called Bachet's equation, after the 17th century mathematician who originally discovered the duplication formula. lt is also sometimes called Mordell's equation, in honor of the 20th century mathematician L. J. Mordell, who made a fundamental contribution to the solution of this and many similar Diophantine equations. We still be proving a special case of Mordell's theorem in Chapter III.
Suppose wo are interested in solutions in rational numbers x, y. An amazing property of this equation is the existence of a duplication fomula, discovered by Bachet in 1621. If (x,y) is a solution with x and y rational, then it is easy to check that
((x4 - 8cx)/(4y2),(-x6 - 20cx3 + 8c2)/(8y3))
is a solution in rational numbers to the same equation. Further, it is possible to prove (although Bachet was not able to) that if the original solution has xy != 0 and if c != 1, -432, then repeating this process leads to infinitely many distinct solutions. So if an integer can be expressed as the difference of a square and a cube of non-zero rational numbers, then it can be so expressed in infinitely many ways. For example, if we start with the solution (3,5) to the equation
y2 - x3 = -2
and apply Bachet's duplication formula, we find a sequence of solutions, that starts
(3 , 5), (129/102 , -383/103), (2340922881/76602 , 113259286337292/76603), ...
As you can see, the numbers rapidly get extremely large.
Next we'll take the same equation
y2 - x3 = c
and ask for solutions in integers x, y. In the 1650's Fermat posed as a challenge to the English mathematical community the problem of showing that the equation y2 - x3 = -2 has only two solutions in integers, namely (3, +/-5). This is in marked contrast to the question of solutions in rational numbers, since we have just seen there are infinitely many of those. None of Fermat's contemporaries appears to have solved the problem, which was solved incorrectly by Euler in the 1730's, and given a correct proof 150 years later! Then in 1908, Axel Thue made a tremendous breakthrough; he showed that for any non-zero integer c, the equation y2 - x3 = c can have only a finite number of solutions in integers x, y.
Fußnote: Axel Thue made important contributions to the theory of Diophantine equations, especially to the problem of showing that certain equations have only finitely many solutions in integers. These theorems about integer solutions were generalized by C. L. Siegel during the 1920's and 1930's. We will prove a version of the Thue-Siegel theorem (actually a special case of Thue's original result) in Chapter V.
This is a tremendous (qualitative) generalization of Fermat's challenge problem; among the infinitely many solutions in rational numbers, there can be but finitely many integer solutions.
The 17th century witnessed Descartes' introduction of coordinates into geometry, a revolutionary development which allowed geometric problems to be solved algebraically and algebraic problems to be studied geometrically. For example, if n is even, then the real solutions to Fermat's equation xn + yn = 1 in the xy plane form a geometric object that looks like a squashed circle. Fermat's Theorem is then equivalent to the assertion that the only points on that squashed circle having rational coordinates are the four points (+/-l, 0) and (0, +/-1). The Fermat equations with odd exponents look a bit different. We have illustrated the Fermat curves with exponents 4 and 5 in Figure 0.1.
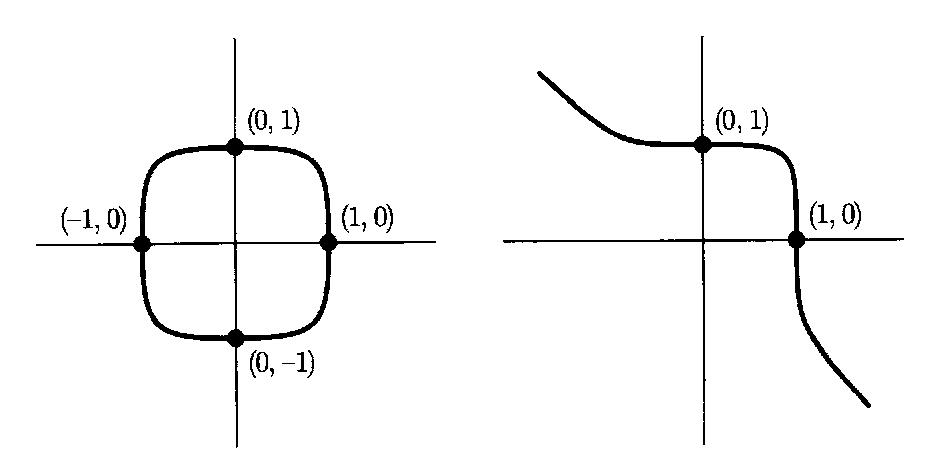
Figure 0.1 The Fermat Curves x4 + y4 = 1 and x5 + y5 = 1
Similarly, we can look at Bachet's equation y2 - x3 = c, which we have graphed in Figure 0.2.
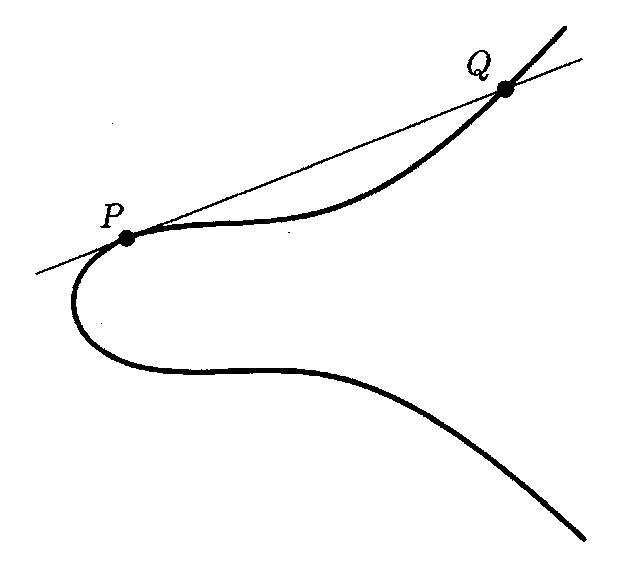
Figure 0.2 Bachet's Equation y2 - x3 = c
Recall that Bachet discovered a duplication formula which allows us to take a given rational solution and produce a new rational solution. Bachet's formula is rather complicated, and one might wonder where it comes from. The answer is, it comes from geometry! Thus, suppose we let P = (x, y) be our original solution, so P is a point on the curve (as illustrated in Figure 0.2). Next we draw the tangent line to the curve at the point P, an easy exercise suitable for a first semester calculus course.
Fußnote: Of course, Bachet had neither calculus nor analytic geometry, so he probably discovered his formula by clever manipulation.
This tangent line will intersect the curve at one further point, which we have labeled Q. Then, if you work out the algebra to calculate the coordinates of Q, you will find Bachet's duplication formula. So Bachet's complicated algebraic formula has a simple geometric interpretation in terms of the intersection of a tangent line with a curve. This is our first intimation of the fruitful interplay that is possible among algebra, number theory, and geometry.
Am Ende von Kapitel 1 kommt dann noch eine Aufgabe:
Beweise, dass Bachets Gleichung für c = 17 genau acht ganzzahlige Lösungen mit y > 0 besitzt.
Versehen mit der Warnung:
This is an extremly difficult problem, and you will almost certainly not be able to do it with the tools we have developed. But it is also an extremly interesting problem which is well worth thinking about.
Gruß
Zaph |
    
Zaph (Zaph)

| | Veröffentlicht am Montag, den 29. Januar, 2001 - 20:49: | 
|
Leider sind mir die Bildchen etwas zu breit geraten :-(
Den Text kann man zwar nachträglich verändern, die Graphiken aber offenbar nicht. |
    
Matroid (Matroid)

| | Veröffentlicht am Montag, den 29. Januar, 2001 - 21:15: | 
|
Hi Zaph,
ich lese noch. Man findet also in Chapter V den Beweis, daß y²-x³ = -2 genau zwei ganzzahlige Lösungen hat?
Danke Matroid |
    
Zaph (Zaph)

| | Veröffentlicht am Freitag, den 02. Februar, 2001 - 21:19: | 
|
Hi Matroid,
Chapter V hat 35 Seiten. Aber wenn ich es richtig gesehen habe, wird dort nicht bewiesen, dass y² - x³ = -2 nur die beiden Lösungen besitzt. Dafür wird dort folgender Satz zitiert (aber nicht bewiesen):
Theorem (A. Baker, 1966) Seien a, b, c ganze Zahlen und sei
H = max{|a|,|b|,|c|}.
Dann ist für jeden Punkt (x,y) auf der elliptischen Kurve
y² = x³ + ax² + bx + c
die Ungleichung
max{|x|,|y|} <= e^((1000000 * H)^1000000)
erfüllt.
Bei Bachets Gleichung ist a = b = 0 und c = -2, also H = 2.
Du brauchst also nur noch endlich viele Fälle durchzuprobieren ;-) |
    
Matroid (Matroid)

| | Veröffentlicht am Freitag, den 02. Februar, 2001 - 22:19: | 
|
Hi Zaph,
das hatte ich befürchtet. Immerhin ist die gestellte Aufgabe nicht trivial, das tröstet mich.
Gruß
Matroid |
    
Zaph (Zaph)

| | Veröffentlicht am Freitag, den 02. Februar, 2001 - 22:35: | 
|
Nein, trivial ist sie schon deshalb nicht, weil Fermat und seine Kollegen sie nicht rausgekriegt haben und auch Euler nur eine fehlerhafte Lösung liefern konnte.
Ob Kilian das wusste ...? ;-) |
    
Martin

| | Veröffentlicht am Samstag, den 24. Februar, 2001 - 14:43: | 
|
Ich hab´ hier ein Buch, da steht der Beweis auf einer halben Seite:
y³=x²+2
Wir zerlegen die rechte Seite der Gleichung in ihre Primfaktoren (siehe unten), diese müssen wegen der links stehenden dritten Potenz Kubikzahlen sein. Aus
y³=(x+iÖ2)(x-iÖ2), 1²=-1
folgt also z.B.
x+iÖ2=(u+viÖ2)³=u³+3u²viÖ2-6uv²-2v³iÖ2.
Der Koeffizientenvergleich des imaginären Teils ergibt
1=3uv²-2v³=v(3u²-2v²),
folglich ist u²=1, u=±1 und v=1.
Der Koeffizientenvergleich des reellen Teils ergibt
x=u³-6uv²=u(u²-6v²)=±1(1-6)=±5.
x²+2=27, y³=27, y=3.
Soweit ist die Aufgabe leicht zu lösen. Aber vorher muss man nachweisen, dass x²+2 für Einsetzungen x=a+biÖ2 mit ganzzahligen a,b eindeutig nur in obige Primzahlen (:in dem betreffenden Ring unzerlegbare Elemente) gespalten werden kann. Dies ist für den hier vorliegenden "Ring Z(iÖ2)" tatsächlich der Fall-ebenso bekanntlich für den Gaußschen Ring Z(i).
In einem anderen Buch habe ich noch den Beweis der letzten Aussage. Wenn man sich die Vielfachen einer Zahl n anschaut (n, 2n, 3n, iÖ2n, 2iÖ2n, (1+iÖ2)n,...), dann sieht man, das sie ein quadratisches Gitter bilden. Jede Zahl ist dann nicht mehr als |n|/Ö2 von dem nächsten Vielfachen der Zahl n entfernt. 1/Ö2 ist kleiner als 1 und deswegen gilt die Tatsache, dass wenn man eine Zahl durch eine andere teilt, man einen kleineren Rest erhält.
Der Rest des Beweises funktioniert dann gleich wie bei den natürlichen Zahlen.
Viele Grüße,
Martin |
|