| Autor |
Beitrag |
    
Klaus (kläusle)

Erfahrenes Mitglied
Benutzername: kläusle
Nummer des Beitrags: 385
Registriert: 08-2002
| | Veröffentlicht am Sonntag, den 09. März, 2003 - 20:17: | 
|
Hi!
Hier die anderen Threads des Exkurses:
Teil 1:
http://www.mathehotline.de/mathe4u/hausaufgaben/messages/9308/255 231.html?1046210374
Teil 2:
http://www.mathehotline.de/mathe4u/hausaufgaben/messages/9308/255 464.html?1046790415
Teil 3:
http://www.mathehotline.de/mathe4u/hausaufgaben/messages/9308/255 613.html?1047240696
MfG Klaus
|
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 485
Registriert: 06-2001
| | Veröffentlicht am Sonntag, den 09. März, 2003 - 21:26: | 
|
So, nachdem wir den 1. Anwendungsteil oder Übungsteil hinter uns gebracht haben können wir nun weiter in der Theorie voranschreiten.
Themen unter anderen sind:
-lin. DGL n-ter Ordnung
-numerisches lösen von DGL's (Euler;Runge-Kutta)
Danach stehen noch zur Verfügung:
-Differentialgleichungssysteme
-Laplace Transformationen
Ab Morgen geht es los;
Gruß N. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 486
Registriert: 06-2001
| | Veröffentlicht am Montag, den 10. März, 2003 - 10:58: | 
|
So, nun geht es weiter in der Theorie:
hom. lin DGL n-ter Ordnung mit veränderlichen Koeffizienten
===============================================
Definition:
Eine lin DGL n-ter Ordnung mit veränderlichen Koeffizienten ist eine DGL der Form:
yn+fn-1(x)yn-1+...+f1(x)y'+f0(x)y=s(x)
fn(x) sind alles in einem Definitionsbereich (a;b) stetige Funktionen
Wenn Störfunktion s(x)=0 ist, so nennt man die DGL homogen, sonst inhomogen.
Wir können viele Eigenschaften, die wir bei homogenen DGL. 2. Ordnung kennengelernt haben auf die DGL n-ter Ordnung "übertragen". Wichtig sind dabei folgende Eigenschaften.
(1) ist y eine Lösung der DGL, so ist auch C*y (C Element R) eine Lösung der DGL.
(2) sind y1 und y2 Lösungen der DGL, so ist auch y=y1+y2 eine Lösung der DGL.Das superpositionsprinzip (Überlagerungsprinzip)
Aus (1) und (2) folgt eine weitere Eigenschaft, nämlich die überlagerung mit Konstanten aber das ist nichts neues:-)
Wichtig ist folgende Eigenschaft:
Wenn yp eine partikuläre Lösung der DgL ist, dann können wir die DGL über die Substitutionen
y=ypz und danach z'=u auf eine DGL (n-1)ter Ordnung "ernidrigen", bzw. reduzieren, zurückführen.
Für uns folgt daraus folgendes Lösungsverfahren:
a)-Wir eraten eine partikuläre Lösung der DGL n.ter Ordnung
b)-durch die Substitution y=yp*z und z'=u ernidrigen wir die DGL um ein Grad auf eine DgL
(n-1)ter Ordnung.
c)-führe a) und b) solange hintereinander aus, bis du auf eine DGL 1. Ordnung stößt, die du lösen kannst.
d) durch a) und b) hast du nacheinander n-partikuläre Lösungen gefunden.Durch mehrmalige Rücksubstitution erhälst du dann die allgemeine Lösung.
Man könnte auch versuchen aus der DGL n-ter Ordnung n verschiedene partikuläre Lösungen zu erraten. Die n-Reihige Wronski Determinante der Funktionen müsste dann wieder ungleich Null sein, sonst wären die Funktionen ja lin. Abhängig, und "Basislösungen" einer DGL, die ein Fundamentalsystem aufbauen müssen voneinander lin. unhabhängig sein. Die Linearkombination aus den n unabhängigen Basislösungen würde dann die allgemeine Lösung bilden.
Wenn es um inhomogene DGL n-ter Ordnung geht, dann ist die allgemeine Lösung der inhomogenen DGL wieder die Summe aus der allgemeinen Lösung der homogenen DGL und der partikulären Lösung der inhomogenen DGL.
Dieses Verfahren ist allgemeingultig, für lin. DGL n-ter Ordnung, ich habe das aber unter den Titel "lin. DGL n-ter Ordnung mit veränderlichen Koeffizienten" geschrieben, weil es noch für den Fall DGL n-ter Ordnung mit Konstanten Koeffizienten spezielle Lösungsverfahren gibt.
Da ihr aber schon bei DGL 2. Ordnung mit veränderlichen Koeffizienten zu kämpfen hattet, denke ich reicht es, wenn ich diesmal nur das allgemeine Lösungsverfahren für diesem Fall beschreibe.
Wenn es um Berechnungen geht, so werden wir uns nur auf lin. DGL n-ter Ordnung mit Konstanten Koeffizienten beziehen.
Es schadet aber nicht ein Beispiel mit konstaten Koeffizienten nach diesem Verfahren durchzurechnen.
=================================================
39) Berechnen sie Die allgemeine Lösung folgender homogenen DGL mit konstanten Koeffizienten nach dem Oben angegebenen verfahren.
y'''-2y''-y'+2y=0
Gruß N. |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 476
Registriert: 10-2002
| | Veröffentlicht am Montag, den 10. März, 2003 - 11:15: | 
|
Hi,
ich bin auch wieder dabei, musste mal ne Pause machen.
Kanni ch bei dieser Dgl nicht sowas wie den Exponentialansatz machen, dass liefert mir doch wieder eine Gleichung (diesmal dritten Grades!)
x^3-2x^2-x+2=0
mit x= 1 , 2 , -1
==> y=C1*ex+C2*e2x+C3*e-x
weiß nich, kann man das so machen?
mfg |
    
Klaus (kläusle)

Erfahrenes Mitglied
Benutzername: kläusle
Nummer des Beitrags: 390
Registriert: 08-2002
| | Veröffentlicht am Montag, den 10. März, 2003 - 11:19: | 
|
Hi Ferdi,
dasselbe habe ich mir auch gedacht
und bin auf das gleiche Ergebnis gekommen!
MfG Klaus
|
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 487
Registriert: 06-2001
| | Veröffentlicht am Montag, den 10. März, 2003 - 11:58: | 
|
Hi Kolegen,
Erstmal stimmt das Ergebnis.
Natürlich habt ihr recht, man kann auch hier wieder mit charakteristischen Gleichungen arbeiten.
Allgemein besitzt eine lin. DGL n-ter Ordnung eine charakteristische Gleichung
n. ten Grades. Das Problem ist nur das gleiche wie wir von der Nullstellenberechung kennen. Haben wir Gleichungen 3. 4. etc Grades, so rät man ja im Allgemeinen auch erstmal eine Nullstelle und macht dann eine Polynomdivison um dan aus der vermutlich einfacheren Gleichung
(n-1)ten Grades die restlichen Nullstellen "rauszufischen".
In dieser Hinsicht besteht eine Analogie zu den von mir oben beschriebenen Verfahren.
Außerdem müssten wir dann wider wenn wir über charakeristische Gleichungen n-ten Grades sprechen auch über diverse Fallunterscheidungen verhandeln. Das wird noch lustig sage ich euch:-)
Gruß N. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 488
Registriert: 06-2001
| | Veröffentlicht am Montag, den 10. März, 2003 - 12:04: | 
|
Außerdem gilt die Idee mit den "Exponentialansatz" zu arbeiten nur für lin. DGL n-ter Ordnung mit "Konstanten Koeffizienten"-bei "veränderlichen Koeffizienten" geht das natürlich nicht so einfach. Da die DGL mit Konstanten Koeffizienten ein Sonderfall der DGL mit veränderlichen Koeffizienten ist, habe ich erstmal das "allgemein gültige Verfahren" beschrieben und wollte, wie gesagt jezt ausfürlich auf den Sonderfall mit Konstanten Koeffizienten eingehen.
Gruß N. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 489
Registriert: 06-2001
| | Veröffentlicht am Montag, den 10. März, 2003 - 13:31: | 
|
Kleine Nachfrage,
müssen wir noch genauer über das Lösen von Gleichungen 3. Grades sprechen oder nicht?
Wenn wir nun über charakeristische Gleichungen sprechen würde ich mich gerne auf den 3. Grad beschränken,d.h wir werden auch kaum mehr als DGL's 3. Ordnung zur Brust nehmen.
Reicht es euch wenn ich euch die notwendigen Fallunterscheidungen mitteile oder sollen wir versuchen sie herzuleiten?
Gruß N. |
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1035
Registriert: 02-2002
| | Veröffentlicht am Montag, den 10. März, 2003 - 13:55: | 
|
Hi Niels
Ich schätze mal die Fallunterscheidungen sind so ähnlich wie bei den DGLs zweiter Ordnung.
1. Fall
3reelle Lösungen der charakteristischen Gleichung
Hier gibts wie man oben sieht keine Probleme.
2. Fall
Genau eine relle Lösung und sonst keine.
Das ist sicher der umständlichste Weg mit Variation der Konstanten usw.
3. Fall
Eine reelle Lösung und zwei konjugiert komplexe.
Hier nimmt man dann sicher Real- und Imaginärteil einer der komplexen Lösungen und die reelle Lösung.
Hab mir das jetzt alles nicht genauestens überlegt, ist nur so eine Vermutung.
MfG
C. Schmidt |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 490
Registriert: 06-2001
| | Veröffentlicht am Montag, den 10. März, 2003 - 15:41: | 
|
Hi Christian,
ja, du hast es fast richtig erkannt:
Fall 1:
Alle Lösungen der charakeristischen Gleichung sind reell und voneinander verschieden.
Allgemeine Lösung der DGL ist die Linearkombination aus den 3 e-Funktionen mit verschiedenen Exponenten.
Fall 2:
Es gibt reelle Mehrfachlösungen:
ist a eine r-fache Nullstelle der Charakeristischen Gleichung in l der DGL, so gibt es r voneinander verschiedene und unabhängigen Funktionen yr=xr-1*ea*x
Mit Variation der Konstanten kann man in der Tat zeigen. Ist a r-fache Nullstelle, der charakeristischen Gleichung, so lässt sich Das C in der Funktion y=C*egreek{a durch ein Polynom (r-1)ten Grades in x ersetzen.
Fall 3:
Es treten Konjugiert komplexe Lösungen auf.
Naja, den Fall kennen wir auch schon von der DGL 2. Ordnung; Wir wissen auch wie man sie über die Eulerische Formel in Sinus bzw Cosinusterme zerlegt.
Damit sind im "Schnelldurchlauf" alle Fallunterscheidungen durchgesprochen und wir können mal wieder mit Aufgaben zur Tat schreiten:-)
=================================================
Aufgaben:
40) Lösen sie folgende DGL:
a)y'''-2y''+2y'-2y=0
b)y'''-4y''-y'+4y=0
c)y4-6y'''+12y''-10y'+3y=0
d)y4+3y''-4y=0
rann an die Buletten Freunde!
Gruß N. |
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1037
Registriert: 02-2002
| | Veröffentlicht am Montag, den 10. März, 2003 - 16:13: | 
|
Hi!
Ich fang mal mit 40b) an, die scheint am leichtesten zu sein 
y=C1ex+C2e4x+C3e-x
MfG
C. Schmidt |
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1038
Registriert: 02-2002
| | Veröffentlicht am Montag, den 10. März, 2003 - 16:23: | 
|
Weiter gehts mit c)
y=C1e3x+C2ex+C3x*e3x+C4x²*e3x
MfG
C. Schmidt |
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1039
Registriert: 02-2002
| | Veröffentlicht am Montag, den 10. März, 2003 - 16:27: | 
|
Zu d)
y=C1ex+C2e-x+C3sin(2x)+C4cos(2x)
MfG
C. Schmidt |
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1040
Registriert: 02-2002
| | Veröffentlicht am Montag, den 10. März, 2003 - 16:33: | 
|
Kann das sein, dass bei a) irgend was mit den Zahlen nicht stimmt??
Da kommt auf jeden Fall bei der charakteristischen Gleichung keine halbwegs vernünftige Lösung raus.
(So müsste ich einen gerundeten Wert nehmen, auf Cardano hab ich irgendwie keine Lust  ) )
MfG
C. Schmidt |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 479
Registriert: 10-2002
| | Veröffentlicht am Montag, den 10. März, 2003 - 16:48: | 
|
Hast recht Christian, da kommt watt ganz schön komisches raus, Cardano würd ich nur nehmen wenn ich langeweile habe, so würd ich mit den gerundeten Ergebnissen rechnen.
mfg
Meine LÖsungen der ch.Gl:
x=1,5436890126920763
x=0,2281554936539615 - 1,1151425080399375·i
x=0,2281554936539615 + 1,1151425080399375·i |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 491
Registriert: 06-2001
| | Veröffentlicht am Montag, den 10. März, 2003 - 16:55: | 
|
Hallo ihr beiden,
ihr habt recht, es muss bei 40a) heißen:
y'''-2y''+y'-2y=0
Gruß N. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 492
Registriert: 06-2001
| | Veröffentlicht am Montag, den 10. März, 2003 - 16:59: | 
|
Also
40b) richtig gelöst.
40c) falsch (Tippfehler???)
40d) richtig gelöst.
Gruß N.
|
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1042
Registriert: 02-2002
| | Veröffentlicht am Montag, den 10. März, 2003 - 17:01: | 
|
Hi!
Das hört sich gut an...
Lösung wäre dann
y=C1e2x+C2sin(x)+C3cos(x)
MfG
C. Schmidt |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 493
Registriert: 06-2001
| | Veröffentlicht am Montag, den 10. März, 2003 - 17:22: | 
|
Hi Christian,
dann hast du mal wieder 40a) richtig gelöst.
Gruß N. |
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1043
Registriert: 02-2002
| | Veröffentlicht am Montag, den 10. März, 2003 - 17:27: | 
|
Hi Niels!
Ja, bei 40c) wollte ich mir Arbeit ersparen indem ich den ersten Summanden 4 mal kopiere und dann nur ein bißchen verändere. Hab dabei aber zwei mal vergessen die 3 wegzustreichen ;)
Muss natürlich so heißen
y=C1e3x+C2ex+C3xex+C4x²*ex
MfG
C. Schmidt |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 494
Registriert: 06-2001
| | Veröffentlicht am Montag, den 10. März, 2003 - 17:51: | 
|
Hi Christian,
Gut, dann ist 40c) auch als korrekt anerkannt. Können wir dann mit inhomogenen DGL's weitermachen?
Gruß N. |
    
Klaus (kläusle)

Erfahrenes Mitglied
Benutzername: kläusle
Nummer des Beitrags: 392
Registriert: 08-2002
| | Veröffentlicht am Montag, den 10. März, 2003 - 18:20: | 
|
Hi ihr drei,
Mensch, da hat man mal 5 Stunden keine Zeit und ihr postet kurz 20 Beiträge ;-)
@Niels: Es kann weitergehen.
MfG Klaus
|
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 495
Registriert: 06-2001
| | Veröffentlicht am Montag, den 10. März, 2003 - 19:06: | 
|
Gut, dann kann es im "mathematischen Quartett" weitergehen...
Integration der lin. inhomogenen DGL n-ter Ordnung mit Konstanten Koeffizienten
=================================================
Im Grunde lösen wir solche inhomogene DGL's wie immer:
-Lösen der dazugehörigen homogenen DGL
-Aufsuchen einer partikulären Lösung der inhomogenen DgL->Lösungsansätze abhängig von Störfunktion.(Ich mache dazu nochmal eine Tabelle Fertig)
-Beides addieren und schon hat man die allgemeinen Lösung der inhomogenen DGL.
Im Verfahren also nichts neues; Wir können gleich mit Übungsaufgaben loslegen!
================================================
Übungsaufgaben:
Lösen sie folgende DGL's
41)y'''-3y'+2y=2*sin(x)+cos(x)
42)y(4)+2y'''-3y''=20x*e2x
Frage: wollen wir noch kurz über "Eigenwerte" sprechen oder nicht?
Gruß N.
|
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 480
Registriert: 10-2002
| | Veröffentlicht am Montag, den 10. März, 2003 - 20:22: | 
|
Hi,
komme grad vom Fussball, die Aufgaben schau ich mir morgen mal an, bin ein wenig müde.
In welchen Zusammenhang meinst du Eigenwerte? Von Matrizen?
mfg |
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1044
Registriert: 02-2002
| | Veröffentlicht am Montag, den 10. März, 2003 - 20:40: | 
|
Hi!
Lösung zu Aufgabe 41)
y=C1e-2x+C2ex+C3xex+1/2*cos(x)
MfG
C. Schmidt |
    
Klaus (kläusle)

Erfahrenes Mitglied
Benutzername: kläusle
Nummer des Beitrags: 393
Registriert: 08-2002
| | Veröffentlicht am Montag, den 10. März, 2003 - 20:45: | 
|
Hi
Dann will ich mich auch mal wieder beteiligen:
41a)
y = C1e-2x + C2xe-x + 0,5cos(x)
MfG Klaus
|
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1045
Registriert: 02-2002
| | Veröffentlicht am Montag, den 10. März, 2003 - 20:48: | 
|
Hi!
42)
y=C1e-3x+C2ex+C3x+C4+(x-11/5)e2x
MfG
C. Schmidt |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 496
Registriert: 06-2001
| | Veröffentlicht am Montag, den 10. März, 2003 - 21:14: | 
|
Also,
@Christian:
Deine lösung für Aufgabe 41) und 42) ist richtig.
@Klaus:
Deine Lösung für 41) ist leider falsch!
@Ferdi:
Nunja, wir haben ja schonmal am Anfang über Anfangswert und Randwertprobleme gesprochen, und dabei habe ich euch ein Anwendungsberecich "unterschlagen", nämlich die 3 Gruppe von Aufgabentypen sind die sogenanten "Eigenwertprobleme". Im Grunde sind sie eine besondere Form der Randwertprobleme, die Differentialgleichungen am Schluss enthalten aber noch ein freihen Parameter. Man interessiert sich nun für spezielle Werte für diesen Parameter, die nicht zu einer trivialen Lösung führen, diese Werte nennt man dann "Eigenwerte".
Gruß N. |
    
Klaus (kläusle)

Erfahrenes Mitglied
Benutzername: kläusle
Nummer des Beitrags: 395
Registriert: 08-2002
| | Veröffentlicht am Dienstag, den 11. März, 2003 - 12:29: | 
|
Hi
ich verabschiede mich von diesem Exkurs.
Zumindest in aktiver form.
Mal sehen, wie ich noch die Zeit dazu finde.
Nächste Woche fängt's Studium an.
Davor noch ein Kurzurlaub...
Viel Spaß noch!!
Und natürlich viel Erfolg!!
@Niels: Danke für soviel Mühe!!
MfG Klaus
|
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 497
Registriert: 06-2001
| | Veröffentlicht am Dienstag, den 11. März, 2003 - 19:43: | 
|
Hi Klaus,
Gut, dann wünsche ich schönen Urlaub.
@Christian&Ferdi:
Wie sieht das aus, wollen wir nun noch die Eigenwertproblematik besprechen oder gleich zur Numerik übergehen.
Entscheidet euch!
Gruß N. |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 489
Registriert: 10-2002
| | Veröffentlicht am Dienstag, den 11. März, 2003 - 21:18: | 
|
Mir solls egal sein. Wir können ruhig das volle Programm durchziehen!
mfg |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 498
Registriert: 06-2001
| | Veröffentlicht am Mittwoch, den 12. März, 2003 - 11:17: | 
|
Ok,
Eigenwertprobleme-Eigenwertaufgaben
================================================
Beispiel:
Eulerische Knicklast-eulerische Knickkräfte
Skizze:
Homogener Stab der Länge l beidseitig gelenkig gelagert, belastet durch eine in Stabrichtung angreifende konstante Druckkraft F.
"Biegegleichung":
y(4)+(F/(E*l))*y''=0
E...Elastizitätsmodul (elastische Materialkonstante)
l...Flächenmoment oder Flächenträgheitsmoment des Stabquerschnitts
E*l...Biegesteifigkeit(Konstante)
bzw wenn µ²=F/(E*l)
y(4)+µ²*y''=0
Da an den Stabenden weder der Stab sich durchbiegen kann, noch ein Flächenmoment bzw Flächenträgheitsmoment besitzt, gelten folgende "Randwertbedingungen".
y(0)=y(l)=0
y''(0)=y''(l)=0
Jezt wird Festgelegt, welche Lösung trivial ist:
Trivial ist die Lösung y=y(x)=0; Diese Lösung erfüllt zwar die DGL hat aber keine physikalische Bedeutung.
Gesucht sind nun die Lösungsfunktionen der DGL:
y(4)+µ²y''=0
außer halt y=0.
Wir fassen diese Gleichung als
hom. lin. DGL 4. Ordnung mit Konstanten Koeeffizienten auf. Lösung ist:
y=C1+C2*x+C3sin(µx)+C4Cos(µx)
über die 4 Randbedingungen erhalten wir folgende Werte für die C's:
C1=C2=C4=0
Es bleibt die Bestimmungsgleichung:
C3*sin(µl)=0
Da Die Lösung trivial wäre, wenn C3 auch Null wäre muss C3 von Null verschieden sein. Es bleibt nur die Gleichung übrig:
sin(µl)=0
Lösung:
µn=np/l (n Element N)
Das sind die Eigenwerte
Die Eigenlösungen oder Eigenfunktionen sind die Funktionen
y=yn=C3*sin(npx/l) (C3=R\{0})
================================================
Aufgabe 43)
Die "Schrödinger-Gleichung"(SG) für den linearen Potentialtopf der länge a lautet:
Y''(x)+(8p²m*E/h²)Y(x)=0
a) geben sie die Eigenwerte und Eigenlösungen (Eigenfunktionen) der Schrödinger-Gleichung an.
b)Lösen sie mit hilfe der Eigenfunktionen aus a) die Schrödinger-Gleichung analytisch!
c)Welche Energie besitzt das Teilchen im Grundzustand (n=1) und im n-abhängigen Zustand?
Lösungshinweise:
1)Y(0)=Y(a)=0
2)Sx=a x=0Y²(x)*delta(x)=1
(in Worten: Die Summe aller "Teilwahrscheinlichkeiten" muss 1 ergeben.)
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
So, nach dem kurzen Ausflug in die Festigkeitslehre und Quantenphysik kommen wir nun zu den numerischen Lösungsverfahren für DGL's.
Gruß N.
|
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1047
Registriert: 02-2002
| | Veröffentlicht am Mittwoch, den 12. März, 2003 - 14:59: | 
|
Hi Niels
Ich weiss leider nicht was ein linearer Potentialtopf ist, kann so irgendwie mit der Aufgabge nicht viel anfangen.
MfG
C. Schmidt |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 498
Registriert: 10-2002
| | Veröffentlicht am Mittwoch, den 12. März, 2003 - 15:06: | 
|
Hi,
geht mir ähnlich, bin ja sowieso kein Physikass. Ich kenne Schrödinger nur von der Chemie her, von der Orbitaltheorie.
mfg |
    
Klaus (kläusle)

Erfahrenes Mitglied
Benutzername: kläusle
Nummer des Beitrags: 398
Registriert: 08-2002
| | Veröffentlicht am Mittwoch, den 12. März, 2003 - 16:39: | 
|
Hi Christian, Ferdi
Hab kurz Zeit gefunden...
Vielleicht macht's das einfacher...
Die Schrödingergleichung stellt eine Gleichung auf, mit der man die Amplituden der Wahrscheinlichkeitswelle in beliebigen - insbesonderen atomaren - Feldbereichen berechnen kann. Sie hat Bedeutung für den Atombau, die chemische Bindung und viele andere Quantenphänomene.
Von der Chemie solltet ihr wissen, dass die Elektronen nur bestimmte Energiezustände annehmen können (n,m,l,s). Die Zustände sind alle quantifiziert. (spielt aber hier jetzt keine besondere Rolle)
Nun ein Auszug von einem Pyhsikbuch:
Mit dem Aufstellen der Schrödinger-Gleichung ist man der realistischen Beschreibung von Quantenobjekten ein großes Stück nähergekommen. Unser Interesse richtet sich hauptsächlich auf das Verständnis der Elektronen in Atomen. Diese Elektronen werden durch elektrische Anziehungskräfte (beschrieben durch das Potential des Kerns) in der Umgebung des Atomkerns festgehalten. Quantenobjekte, die durch ein Potential auf einen bestimmten Raumbereich eingeschränkt sind, nennt man gebunden.
Quantenobjekte zeigen eine Reihe von neuen, verblüffenden Effekten, wenn sie in einen beschränkten
Raumbereich „eingesperrt“ werden. Dazu gehören die Quantisierung der Energie und der Tunneleffekt. Diese Phänomene sollen in den folgenden Abschnitten untersucht werden. Um zunächst ein Gespür für die neuen Effekte zu entwickeln und die Umstände zu verstehen, unter denen sie auftreten, soll zuerst ein einfaches Modell für gebundene Elektronen betrachtet werden. In der Folge können wir dann zu komplizierteren und realistischeren Systemen übergehen.
Als Prototyp für gebundene Systeme, an dem . alle wesentlichen Züge schon klar hervortreten,
betrachten wir Elektronen, die in einem Potentialtopf gebunden sind. Damit bezeichnet man
den in Abb. 8.12 gezeigten Potentialverlauf. Ein Elektron ist in einen Raumbereich der Breite . eingesperrt, aus dem es nicht entkommen kann: Die „Wände“ des Potentialtopfs bilden eine undurchdringliche Barriere; das Potential geht dort gegen Unendlich. Im Innern des Potentialtopfs
(d. h. für ) sollen dagegen auf die Elektronen keine Kräfte einwirken. Das Potential
besitzt hier einen konstanten Wert.
MfG Klaus
|
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 499
Registriert: 06-2001
| | Veröffentlicht am Mittwoch, den 12. März, 2003 - 18:22: | 
|
Grrr, das ist natürlich schlecht, na gut, dann erkläre ich den Potentialtopf:
Wir Sprechen vom linearen Potentialtopf, d. h. das Teilchen befindet sich auf eine art Seil, das zwischen 2 Wänden, den Wänden des Potentialtopfes, gespannt ist. Dort schwingt das Teilchen also nur in einer Richtung auf dem Seil.
Bedingung 1:
Im Potentialtopf ist die potentielle Energie Null.
Epot=0
Alle Energie, die das Teilchen besitzt setzt das Teilchen in kinetische, sprich Bewegungsenergie um:
E=Ekin=0,5mv²=p²/2m (1)
p...Impuls des Teilchens
Bedingung 2:
Aus der Quantenphysik wissen wir, das prinzipiell jeder Gegenstand eine Wellenlänge besitzt, die sogenante De Broglie Wellenlänge:
l=h/p (2)
h...planksches Wirkungsquantum
Daraus folgt
p²=h²/l²
Dies in (1) Eingesetzt ergibt:
E=h²/(2ml²) (3)
Nun ist es so, das Teilchen schwingt ja auf einen Seil, das an beiden Potentialtopfwänden fest ist, das heißt, wenn es schwingt, dann als "Stehende Welle". Für stehende Welle gilt folgende Bedingung:
a=0,5*n*l (4)
woraus folgt:
l²=4a²/n² (4)
setzt man nun (4) in (3) ein so erhält man für die Energie eines Teilchens im Potentialtopfes:
En=h²n²/(8ma²)
============================================
Diese Formel stellt die Lösung von Aufgabe 43c) dar.
Für die in Aufgabe 43b) gefragte Lösungsfunktion muss sich genau diese Bedingung ergeben, sonst ist sie nicht eine Lösungsfunktion der Schrödinger Gleichung.
Es geht mir aber nicht darum das ihr schrödinger versteht, sondern "nur" darum, das ihr sie löst.
Mein Lehrer würde sagen, ihr müsst das Problem "transformieren"; Wenn ihr die Biegegleichung und die Schrödingergleichung miteinander vergleicht, so solltet ihr einige ähnlichkeiten finden!
Versucht es mal!
@Christian:
Was ist das denn, Physik LK und noch kein Schrödinger drangekommen? hattet ihr noch nicht Quantenphysik? Bei uns in S-H war Quantenphysik in 12.2 dran. Und das sogar mit Schrödinger im GK! (Ich habe ja nur GK Physik)
@Ferdi,
Der Schrödinger aus der Chemie ist der gleiche, der diese schöne Gleichung 1926 erfand.Sein voller Name ist ERWIN SCHRÖDINGER. Er hat zusammen mit HEISENBERG 1932 den Nobelpreis für Physik bekommen.Heisenberg hat mit Matrizen gerechnet und Schrödinger über DGL's und beide hatten nachher das gleiche Ergebnis raus und klopten sich anschließend welches Ergebnis besser ist:-)
Das Orbitalmodell aus der Chemie beschreibt ja prinzipell nicht anderes als Antreffwahrscheinlichkeiten, genauso wie schrödingers Y²(x) Wellenfunktion. Nur das richtige Orbitalmodell ist noch komplizierter als der 3-D Potentialtopf, und wir reden hier bloß vom linearen also eindimensionalen Potentioatopf...
Gruß N.
|
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 500
Registriert: 06-2001
| | Veröffentlicht am Donnerstag, den 13. März, 2003 - 09:42: | 
|
Seit ihr jetzt in der Lage Aufgabe 43) zu lösen oder nicht?
Wie gesagt, es gehr mir nur um die Mathematik die hinter Schrödinger steht, für Tiefere Verständnisfragen zur Quantenphysik bin ich
a) nicht genügend qualifiziert sie zu beantworten und b) sind wir eh im falschen Forum eigentlich.
Ihr müsst ganz prakmatisch an die Aufgabe rangehen. Follgende Fragestellungen könnten hilfreich bei der Lösung sein?
-Welcher "Term" wird wohl mit µ² substituiert?
-Welche Lösung der Schrödingergleichung ist trivial?
-Wieviele "Randwerte" brauche ich zur Lösung und welche Randwerte habe ich aus welchen Gründen vorgegeben?
Gruß N.
|
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1049
Registriert: 02-2002
| | Veröffentlicht am Donnerstag, den 13. März, 2003 - 14:19: | 
|
Hi Niels
Was ist das denn, Physik LK und noch kein Schrödinger drangekommen? hattet ihr noch nicht Quantenphysik? Bei uns in S-H war Quantenphysik in 12.2 dran. Und das sogar mit Schrödinger im GK! (Ich habe ja nur GK Physik)
Den Potentialtopf haben wir irgendwie in der Quantenphysik ausgelassen, den Rest den du oben geschrieben hast ist mir schon bekannt 
Unser GK hat den übrigens auch gemacht, ich weiss nicht warum wir den ausgelassen haben...
Ich werd die Aufgabe dann später nochmal versuchen, hab aber leider grad keine Zeit.
MfG
C. Schmidt |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 501
Registriert: 06-2001
| | Veröffentlicht am Donnerstag, den 13. März, 2003 - 17:16: | 
|
Hallo kolegen,
folgender Link
http://siux00.physik.uni-siegen.de/~brandt/Schroed inger/sld019.html
bietet Hintergrundinformationen über Schrödinger, seine Gleichung und Quantenphysik generell.
Nimt man (10) auf der Folie und multipliziert sie mit (8p²m/h²) durch, so erhält man
Y''(x)+(8p²m*/h²)*(E-V)Y(x)=0
Da V als potentielle Energie im linearen Potentialtopf Null ist, folgt daraus die in Aufgabe 43) genannte Form der Schrödinger Gleichung(SG). Trotzdem solltet ihr die Aufgabe selber lösen...
Gruß N.
|
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1050
Registriert: 02-2002
| | Veröffentlicht am Donnerstag, den 13. März, 2003 - 17:19: | 
|
Hi!
Ich glaube ich habe es jetzt verstanden.
Trivial ist y(x)=0.
Dann habe ich substituiert
m²=8pmE/h²
Also Lösung der DGL erhält man damit
y=C1cos(mx)+C2sin(mx)
Mit Randbedingungen muss noch gelten
C2sin(ma)=0
Damit die Lösung nicht trivial wird ist
mn=np/a
Also sind die Eigenfunktionen zu den Eigenwerten mn:
yn(x)=C2sin(mnx)
Das sollte die a) gewesen sein.
Bei der b) hab ich jetzt deinen zweiten Hinweis benutzt, d.h. ich habe das Integral von 0 bis a von den Eigenfunktionen hoch zwei gebildet und gleich 1 gesetzt. Damit erhält man dann den Wert von C2.
Der ist C2=sqrt(2/a)
Also hat man
yn(x)=sqrt(2/x)*sin(np/a*x)
Rechnet man damit E aus kommt das gleiche raus wie bei dir.
MfG
C. Schmidt |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 502
Registriert: 06-2001
| | Veröffentlicht am Donnerstag, den 13. März, 2003 - 17:36: | 
|
Hi Christian,
exat!!!
Du hast anscheined Schrödinger verstanden und Aufgabe 43) komplett richtig gelöst. Den Grund für die Randbedingungen habe ich im Prinzip auch schon genant. Wegen der Bedingung das das Teilchen als "stehende Welle" schwingt, müssen an den Wänden des Potentialtopfes sogenante "Schwingungsknoten" existiteren. Daher gilt.
Y(0)=Y(a)=0
=================================================
Ich finde, das dies eine sehr anspruchsvolle Aufgabe war; also grade richtig für uns:-)
Gruß N.
|
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 503
Registriert: 06-2001
| | Veröffentlicht am Donnerstag, den 13. März, 2003 - 17:42: | 
|
Dann können wir ja zu den numerischen Verfahren kommen oder?
Gruß N. |
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1051
Registriert: 02-2002
| | Veröffentlicht am Donnerstag, den 13. März, 2003 - 17:44: | 
|
Ja, von mir aus schon |
    
Ferdi Hoppen (tl198)

Senior Mitglied
Benutzername: tl198
Nummer des Beitrags: 502
Registriert: 10-2002
| | Veröffentlicht am Donnerstag, den 13. März, 2003 - 19:55: | 
|
Puh,
hab heute meine Abschlussklausur in Chemie geschrieben, über wirklich alles! Schrödinger, Farbentheorie, Redoxsysteme, meine Herren, da noch ins mündlich Abi, naja...
Von mir aus können wir auch weiter machen...
mfg |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 504
Registriert: 06-2001
| | Veröffentlicht am Freitag, den 14. März, 2003 - 13:25: | 
|
OK, kollegen, es geht los:
Numerische Integration einer DGL 1. Ordnung
================================================
Eigentlich hätte ich jetzt mit einem Sturm der Entrüstung und Empörung gerechnet-numerische Integration einer DGL 1. Ordnung geht doch gar nicht!!!
Geht auch nicht:-)
Ihr hättet ja recht gehabt, die Formulierung ist missverständlich. Eine numerische Integration einer DGL 1. Ordnung ist nicht möglich, weil die Lösungsmenge eine Funktionsschar ist. Und die Aufstellung einer "Näherungsschar" ist nicht möglich. Was wir aber machen können ist, wir können uns durch ein "Anfangswertproblem" das wir zusammen mit der DGL formulieren, eine Lösungsfunktion aus der Lösungsschar "herauspicken" und die dann durch eine andere Funktion näherungsweise berechnen, wir können immer nur zu einer speziellen Funktion eine "Näherungsfunktion" eine "Näherungskurve" bestimmen.
Das "Streckenzugverfahren" von Euler
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Gegeben ist also die DGL 1. Ordnung
y'=f(x;y)
mit dem Anfangswert
y(x0)=y0
Wir können dieses "Anfangswertproblem" nur in einem speziellen Intervall
a=<x=<b
lösen.
Dazu teilen wir das Intervall in n Teile
h=(b-a)/n
wobei h im allgemeinen als "Schrittweite" bezeichnet wird.
Es gilt:
x0=a
x1=x0+h
x2=x0+2h
...
xn=b
also allgemein
xk=x0+k*h (k=0,1,....,n)
Ausgehend vom Ausgangspunkt
P0(x0|y0) der auf der exakten Lösungskurve y=y(x) liegt, ersetzen wir die Lösungskurve im intervall x0=<x=<x1 näherungsweise durch die Kurventangente im Punkt P0.Für die Steigung der Tangente gilt
(y-y0)7(x-x0)=m0=f(x0;y0)
Es gilt somit die Gleichung der Tangente:
y=y0+(x-x0)*f(x0;y0)
An der Stelle x1=x0+h besitzt diese Tangente den Ordinatenwert:
y1=y0+h*f(x0;y0)
Damit haben wir einen neuen Punkt
P1(x1|y1) dessen Koordinaten die Grundlage für die weitere Analoge Rechnung für das Intervall x1=<x=<x2 bildet.Nach insgesammt n Rechenschritten ist man Fertig, und kann die Punkte miteinander verbinden. Allerdings sind diese Verbindung zwischen 2 Punkten ja Gerade, sie bilden Strecken, deswegen heißt das Verfahren auch "Streckenzugverfahren".Natürlich wird dieser streckenzug umso genauer, je kleiner h ist, dadurch wird aber die Anzahl an Rechenschritten stehts größer und damit auch der Rechenaufwand größer, daher ist das Verfahren für die Praxis eher ungeeignet.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
=================================================
Aufgabe 44)
Gegeben ist das Anfangswertproblem:
y'=y+ex y(0)=1
a)lösen sie Das Anfangswertproblem analytisch!
b)lösen sie das Anfangswertproblem numerisch im Intervall 0=<x=<0,2 für die Schrittweite h=0,05!
c) Führen sie eine analoge Rechnung wie in b) für die Schrittweite h=0,025 durch!
d)Vergleichen sie die numerischen mit den exakten Werten! werden für kleinere h die Werte wirklich genauer?
viel Spaß!
Gruß N.
|
    
Ferdi Hoppen (tl198)

Senior Mitglied
Benutzername: tl198
Nummer des Beitrags: 504
Registriert: 10-2002
| | Veröffentlicht am Freitag, den 14. März, 2003 - 14:50: | 
|
also wenn mans analytisch macht,
müsste wenn ich mich nicht verrechnet hab:
y=(x+C)ex rauskommen,
und mit y(0)=1
1=(0+C)*1
C=1
also:
y=(x+1)ex
erst ma das
mfg |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 505
Registriert: 06-2001
| | Veröffentlicht am Freitag, den 14. März, 2003 - 15:57: | 
|
Hi Ferdi,
deine analytische Lösung ist schonmal richtig!
kannst weiterrechnen!
Gruß N. |
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1054
Registriert: 02-2002
| | Veröffentlicht am Samstag, den 15. März, 2003 - 13:19: | 
|
Hi!
Ich versuch mal die b), bin mir aber nicht sicher, ob ich mich nicht irgendwo verrechnet hab.
P0=(0|1)
P1=(0,05|1,1)
P2=(0,1|1,155+0,05e0,05)
P3=(0,15|1,21275+0,0525e0,05+0,05e0,1)
P4=(0,2|1,2733875+0,055125e0,05+0,05250,1+0,050,15)
Das sind meine 4 Punkte.
MfG
C. Schmidt |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 506
Registriert: 06-2001
| | Veröffentlicht am Samstag, den 15. März, 2003 - 13:41: | 
|
Hi Christian,
deine 4 Punkte sind richtig!
Wenn du diese 4 Punkte als "Polygonzug" miteinaner verbinden würdest, würde dieser Streckenzug eine zugegeben sehr grobe Näherungskurve geben.
Gruß N. |
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1055
Registriert: 02-2002
| | Veröffentlicht am Samstag, den 15. März, 2003 - 14:17: | 
|
Hi!
Ich hab bei der zweiten Aufgabe jetzt mal die Werte für die Punkte gerundet.
P0=(0|1)
P1=(0,025|1,050)
P2=(0,05|1,102)
P3=(0,075|1,156)
P4=(0,1|1,212)
P5=(0,125|1,269)
P6=(0,15|1,330)
P7=(0,175|1,392)
P8=(0,2|1,457)
Die ganzen Werte habe ich jetzt mit den exakten verglichen. Für kleinere h ist man näher am exakten Wert dran 
MfG
C. Schmidt |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 507
Registriert: 06-2001
| | Veröffentlicht am Samstag, den 15. März, 2003 - 14:51: | 
|
Hi Christian,
Deine Punkte sind alle korrekt und das wie gesagt die Werte führ sehr kleine h den Exakten Werten immer näher kommen habe ich ja oben schon angekündigt. Das Problem ist nur wie gesagt, je kleiner h ist umso mehr n gibt es und das Bedeutet mit der größeren Genauigkeit wächst auch der Rechenaufwand.
Wir werden daher noch ein numerisches Verfahren kennenlernen, das im Verhältnis zum Rechenaufwand recht brauchbare Näherungen lifert.
Dazu müssen wir aber vorher noch ein paar Begriffe klären, ja und dann nach diesem netten Näherungsverfahren wären wir praktisch durch mit dem Exkurs!
Jedenfall was dann "gewöhnliche DGL's" betrifft. Wir könnten dann noch bei Bedarf einen 2. Anwendungsteil hinterherschieben, wo es dann hauptsächlich um DGL 2. und höherer Ordnung geht. wieder ein kleines Testprogramm, damit man sehen kann was ein dieser Exkurs gebracht hat.
Wenn ihr wollt könnten wir das Thema auch noch ausdehnen zu den Differentialgleichungssystemen und Laplace Transformationen, aber das müsst ihr wissen was ihr machen wollt. Ich biete wie gesagt diese beiden Themen als "Anschlußexkurs" an.
Ansonsten könnten wir dann nächste Woche das Sommersemester 2002/2003 zum Thema "gewöhnliche Differentialgleichungen" zum Abschluß bringen.
Für heute ist aber erstmal Schluss, ich muss nämlich gleich noch zu einem Geburtstag.
Runge-Kutta und Co. führen wir uns dann Morgen zu Gemüte.
Gruß N.
|
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 512
Registriert: 06-2001
| | Veröffentlicht am Montag, den 17. März, 2003 - 21:32: | 
|
Ein kleiner Einschub ist an dieser Stelle Notwendig:
Linienelemente-Isoklinie-Richtungsfelder
===============================================
Ein paar geometrische Abschlußbetrachtungen sind notwendig um nachher mit Runge-Kutta fortzufahren.
Die Differentialgleichung y'=f(x,y) besitzt die Eigenschaft, das durch jeden Punkt
P0(x0|y0) des Definitionsbereich eine Lösungskurve verläuft.
Wir können jetzt die Steigung in jeden
Punkt P0 entweder errechnen, indem wir die Ausgangsfunktion differenzieren oder die dazugehörige DGL integrieren.Wir können also die Kurventangente in jeden Punkt P0 zeichnen.
Dieses macht man auch in der Praxis.
Man berechnet in vielen Punkten des Definitionsbereich die Steigungen und deutet diese als Kurventangentenstücke, die dan Linienelemente genannt werden, an.
Das Bild was durch viele dieser "Linienelemente" entsteht wird als Richtungsfeld der DGL bezeichnet.Aus dem Richtungsfeld der DGL kann man häufig Rückschlüsse über den Verlauf der Lösungskurve ziehen.Das ist nützlich, wenn man eine DGL numerisch lösen möchte.
Unte isoklinien versteht man nun die Verbindungslienie von allen Linienelementen, die in der selben/gleichen Richtung verlaufen. Für die Isoklinien gilt die Bedingung:
f(x;y)=y'=Konstant=a.
Ein Beispiel:
Wir nemen die DGL
x+yy'=0
Wir berechnen die Isoklinien:
Aus der DGL wird:
x+ay=0
für a=0 =>x=0
für a<>0=>-x/a
Man erkennt das die Isoklinien alles Ursprungsgeraden sind, und aus dem Richtungsfeld erkennt man, da die Lösungskurven alles konzentrische Kreise um den Ursprungs sind. Ein Ergebnis, was wir aus früheren Rechnungen nur bestätigen können.
================================================
Aufgabe 45)
Gegeben ist die DGL:
y'=2x
a)Zeichne das Richtungsfeld der DGL
b)berechne die Isoklinien der DGL
c)Wie müsste ihrer Meinung nach, nach der Analyse von a) und b) eine Lösungskurve aussehen?
d)Lösen sie die DGL analytisch!
46) Skizzieren sie das Richtungsfeld folgender DGL's mit hilfe von Isoklinien! Versuche sie die Lösungskurve einzuzeichnen und zu beschreiben! Anschließend löden sie die DGL's analytisch!
a)y'=0,5(y/x) x>0
b)y'=y
Die Aufgabne Herrschaften sind nicht unlösbar;sie sind eher primitiv einfacher Natur. Worum ich diesmal aber bitte ist die Einhaltung der Reihenfolge der Aufgaben. erst 45a) dan 45b) und so weiter. Das gleiche gilt für die Ausführung der Anweisungen für Aufgabe 46) sons ist es ja viel zu billig....
viel Spaß beim zeichnen!
Gruß N. |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 513
Registriert: 06-2001
| | Veröffentlicht am Montag, den 17. März, 2003 - 21:37: | 
|
sorry Kollegen, aber Sontag Abend ist das Board ausgefallen-daher die Verzögerung!
Trotzdem viel Vergnügen beim Rechnen....
Gruß N. |
    
Ferdi Hoppen (tl198)

Senior Mitglied
Benutzername: tl198
Nummer des Beitrags: 514
Registriert: 10-2002
| | Veröffentlicht am Dienstag, den 18. März, 2003 - 11:58: | 
|
Hm,
irgendwie hab ich mal wieder ein Brett vorm Kopf.
Wenn ich y'=2x habe, soll ich dann integrieren um die Steigungen der Tangente zu berechnen? oder welche ist die Ausgangsfunktion (die Lösungsfunktion?) und diese ableiten? Und wie soll ich Bilder hier hochladen, das funzt zu 99,9999% nie bei mir!
Also, ich würd sagen wenn ich mir die Aufgabe 45 anschaue, sieht man das eine Parabelschar entsteht, und das soll man mit dem Richtungsfeld erkennen können?
mfg |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 515
Registriert: 06-2001
| | Veröffentlicht am Dienstag, den 18. März, 2003 - 12:25: | 
|
Hi Ferdi,
nein, nicht integrieten-d.h noch nicht integrieren-Ich habe nur geschildert, wie man jetzt, Steigungen allgemein auf 2 verschiedene weisen berechnen kann.
Beispiel:
y'=2x
dann nimmst du dir irgend ein x Koordinante vor:
Beispielsweise x0=3 dann beträgt die Steigung in allen Punkten die auf der Geraden x=3 liegen ja m=6. in anderen Koordinanten von x ist die Steigung anders. so entsteht ein Richtungsfeld.
versuchs mal!
übrigens Grafik:
Entweder sind dann deine Bilder zu groß von der Kb zahl her oder sie sprengen den Ramen von 1200X800 pics.
Gruß N. |
    
Ferdi Hoppen (tl198)

Senior Mitglied
Benutzername: tl198
Nummer des Beitrags: 516
Registriert: 10-2002
| | Veröffentlicht am Dienstag, den 18. März, 2003 - 17:53: | 
|
Hi,
also ich ab jetzt soviel versucht:
hab mich mal umgeschaut.
meinst du sowas:
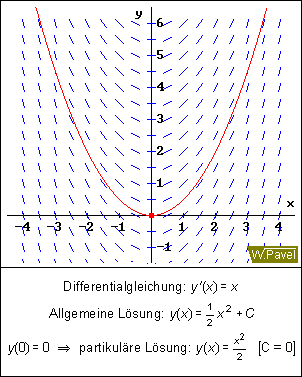
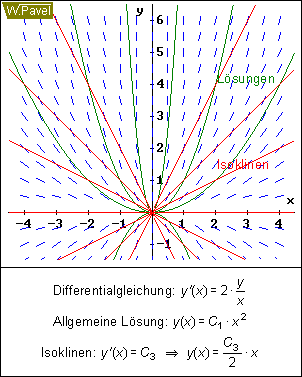
mfg |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 517
Registriert: 06-2001
| | Veröffentlicht am Dienstag, den 18. März, 2003 - 18:16: | 
|
Hi Ferdi,
genau so etwas meine ich!
Erinnert irgendwie an ein Magnetfeld, derren "Magnetfeldlinien" man mit eisenspäne sichtbar macht, oder an elektrische Feldlinien, die man durch Grießkörner in Öl darstellen kann.
Aus diesen Richtungsfeldern und isoklinien kann man, wie schon erklärt,Näherungskurven für die Lösungsfunktion ablesen.
Deine Bildchen mit den Richtungsfeldern stellen aber Richtungsfelder dar, die zu Funktionen und DGL's gehören, die nicht gefragt waren. die DGL's in den Aufgaben sind andere-also gibt es andere Richtungsfelder.
Prinzipiell hast du aber alles richtig verstanden.
Gruß N. |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 518
Registriert: 06-2001
| | Veröffentlicht am Mittwoch, den 19. März, 2003 - 11:24: | 
|
Hi Kollegen,
meint ihr, ihr bekommt Aufgaben 45) und 46) noch hin oder wollen wir gleich mit Runge-Kutta weitermachen?
Gruß N. |
    
Ferdi Hoppen (tl198)

Senior Mitglied
Benutzername: tl198
Nummer des Beitrags: 518
Registriert: 10-2002
| | Veröffentlicht am Mittwoch, den 19. März, 2003 - 12:13: | 
|
Von mir aus können wir auch anfangen, also ich hab hier ein wenig an den Aufgaben rumgedoktort. Also, dann ma ran an Runge-Kutta...
mfg |
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1061
Registriert: 02-2002
| | Veröffentlicht am Mittwoch, den 19. März, 2003 - 15:47: | 
|
Von mir aus kanns auch weitergehen. Hatte eben mal wieder Zeit die Aufgaben zu lösen.
MfG
C. Schmidt |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 520
Registriert: 06-2001
| | Veröffentlicht am Samstag, den 22. März, 2003 - 09:30: | 
|
Hallo Kollegen,
entschuldigt das ich jetzt erst Zeit finde, aber die Weltpolitische Lage-sprich der lang erwartete Irak Krieg-hat doch meine Zeitplanung ein wenig zu nichte gemacht.Jetzt aber zu Runge Kutta.
Das Runge-Kutta Verfahren 4. Ordnung
==============================================
Das Runge-Kutta Verfahren ist ein sehr brauchbares Näherungsverfahren für die Lösung von lin. DGL's 1. Ordnung. Es wurde vor ca. 100 Jahren von einem gewissen C. RUNGE und W. KUTTA entwickelt.
Gegeben ist die Funktion:
y'=f(x;y) und der Anfangswert P0(x0|y0)
Das Ergebnis wird wieder eine Gerade sein, derren Steigung sich als mittlere Steigung aus vier anderen Steigungswerten berechnen läst.Das ist auch der Grund, warum man von Verfahren 4. Ordnung spricht.
Die vier Steigungen setzen sich aus den Steigungen in den Randwerten d.h also im Punkt
P0(x0|y0) und P1(x1|y1)
wobei x1=x0+h ist,h ist mal wieder sie Schrittweite des Intervalls.
Ich beschreibe mal wie man geometrisch vorgeht:
wir beginnen im Anfangspunkt P0, die Tangente in diesem Punkt, das Linienelement a, hat die Steigung m1=y'=f(x0;y0).
Man geht nun von P0 aus gradlinig in Richtung des Linienelementes a,also in Richtung der Tangenten und erreicht in der Intervallmitte den Punkt Q
Q(xQ|yQ)=(x0+(h/2)|y0+0,5*h*f(x0;y0)
der Blaue Term wird mit k1 abgekürzt.
k1=h*f(x0;y0)
für yQ ergibt sich dann der Term
yQ=y0+(k1/2)
und für die Steigung in Punkt Q ergibt sich:
m2=f(x0+(h/2);y0+(k1/2))
Dies ist die Steigung des Linienelements b im Punkt Q.
Man geht nun wieder von dem Anfangspunkt P0 aus, diesmal aber Parallel zum Linienelement b, geradlinig wieder bis zur Intervallmitte.Man erreicht so den Punkt R mit den Koordinaten:
R(xR|yR)=(x0+(h/2)|y0+0,5*h*f(x0+(h/2);y0+(k1/2))
der Rote Term wird mit k2 abgekürzt.Für
yR ergibt sich dann folgender Term.
yR=y0+(k2/2).
Die Lösungskurve durch R besitzt in R das Linienelement c, das wiederum die Steigung
m3=f(x0+(h/2);y0+(k2/2))
Wir wandern wieder zurück zum
Anfangspunkt P0. Unser Weg führt uns gradlinig und parallel zum Linienelement c bis zum Intervallende. Wir erreichen
den Punkt S=P1 mit den Koordinaten
xs=x1=x0+h und
ys=y1=y0+h*f(x0+(h/2);y0+(k2/2))
Der grüne Term wird mit k3 abgekürzt.
k3=h*f(x0+(h/2);y0+(k2/2))
Für ys=y1 ergibt sich dann der Term
ys=y1=y0+k3
Die Lösungskurve durch S=P1 besitzt an dieser Stelle das Linienelement d mit der Steigung
m4=f(x0+h;y0+k3
Die Gerade g, die von Ánfangswert P0 bis
zum Punkt S=P1 hat dann die mittlere Steigung
m=(m1+2m2+2m3+m4)/6
Unter der Bedingung, das der Punkt S=P1
die Koordinaten
xs=x1=x0+h
ys=y1=y0+h*f(x0+h;y0+k3)
Der Violette Term wird mit k4 bezeichnet.
k4=h*f(x0+h;y0+k3)
Durch die Mittlung der Steigung ergibt sich für die Gerade die die Näherung der Kurve darstellt der Term
Runge Kutta 4. Ordnung:
y(x1)~y1=y0+(1/6)(k1+2k2+2k3+k4)
Das Verfahren ist deswegen so genau, weil er Fehler ungefähr proportional zu h4 ist.
================================================
Aufgabe 47)
Löse das Anfangswertproblem
y'=y+ex
y(0)=1
numerisch im bereich 0=<x=<0,2 (h=0,05)
Aufgabe 48)
Löse Aufgabe 47) im gleichen Intervall, diesmal aber mit der höheren Näherung h=0,025 .
Vergleiche die Ergebnisse mit dem des Euler Verfahrens!
Gruß N.
|
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 521
Registriert: 06-2001
| | Veröffentlicht am Sonntag, den 23. März, 2003 - 09:42: | 
|
Hi Ferdi, Christian,
wo seit ihr denn?
Gruß N. |
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1069
Registriert: 02-2002
| | Veröffentlicht am Sonntag, den 23. März, 2003 - 12:53: | 
|
Hi!
Hatte wenig Zeit in den letzten Tagen. Hier mal meine Lösung für h=0,05:
P1=(0,05|1,103834644)
P2=(0,1|1,215687995)
P3=(0,15|1,336109356)
P4=(0,2|1,465683310)
h=0,025:
P1=(0,025|1,050947998)
P2=(0,05|1,103834650)
P3=(0,075|1,158725460)
P4=(0,1|1,215688007)
P5=(0,125|1,274792008)
P6=(0,15|1,336109377)
P7=(0,175|1,399714301)
P8=(0,2|1,465683306)
Das Verfahren ist auf jeden Fall sehr genau und viel genauer als das Eulerverfahren.
MfG
C. Schmidt |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 522
Registriert: 06-2001
| | Veröffentlicht am Sonntag, den 23. März, 2003 - 18:25: | 
|
Hi Christian,
deine Ergebnisse sind richtig!
das schöne an diesem Runge-Kutta verfahren ist, das es auch für lin. DGL's leicht abgewandelt anwendbar ist.Dabei bleiben aber die "Gewichtungen" wie bei Runge Kutta für lin. DGL 1. Ordnung erhalten, wenn es um die berechnungen der mittleren Steigung etc geht.
versuche es mal!
Aufgabe 49)
Lösen sie das Anfangswertproblem
y''=y'+2y
y(0)=3
y'(0)=0
im Bereich 0<x<0,3 mit der Schrittweite h=0,1
numerisch!
Aufgabe 50)
Lösen sie das Anfangswertproblem aus Aufgabe 49) exakt und vergleichen sie die numerischen mit den exakten Werten!
=================================================
So, Herrschaften das war's!!!!!!!!!
Das war die lezte Aufgabe zu diesem Exkurs!
Jezt würden normalerweise lin. DGL Systeme folgen. Wenn gewünscht geht es weiter-allerdings in einem neuen Beitrag. Ansonsten schließe ich hier den Exkurs oder wollt ihr noch ein Abschluß Anwendungsteil?
Das ist alles eure Entscheidung!
Entscheidet euch!
viel Spaß noch...
Gruß N.
|
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1071
Registriert: 02-2002
| | Veröffentlicht am Montag, den 24. März, 2003 - 13:57: | 
|
Hi!
49)Ich versuch mich mal mit folgenden Näherungswerten:
P1=(0,1|3,031075)
P2=(0,2|3,129279762)
P3=(0,3|3,303755241)
50)
Lösung des Anfangswertproblems ist
y=2e-x+e2x
Damit erhält man folgende Punkte:
P1=(0,1|3,031077594)
P2=(0,2|3,129286204)
P3=(0,3|3,303755241)
MfG
C. Schmidt
|
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 523
Registriert: 06-2001
| | Veröffentlicht am Montag, den 24. März, 2003 - 16:21: | 
|
Hi Christian,
deine Werte sind richtig, aber nicht vollständig!
wie lauten die Näherungswerte für y' an den einzelnen Stellen?
Gruß N. |
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1075
Registriert: 02-2002
| | Veröffentlicht am Freitag, den 28. März, 2003 - 10:38: | 
|
Hi Niels
Endlich geh das Forum mal wieder 
Hier meine Werte für y' an den einzelnen Stellen:
y'(0,1)=0,633125
y'(0,2)=1,346174118
y'(0,3)=2,162576070
MfG
C. Schmidt |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 524
Registriert: 06-2001
| | Veröffentlicht am Freitag, den 28. März, 2003 - 12:09: | 
|
Hi Christian,
deine Werte sind richtig.
Wie soll es mit dem Exkurs weitergehen?
Wollen wir ihn nun an dieser Stelle beenden oder wollen wir mit DGL Systemen weitermachen?
Gruß N. |
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1076
Registriert: 02-2002
| | Veröffentlicht am Freitag, den 28. März, 2003 - 12:59: | 
|
Hi Niels
Also mich würden auf jeden Fall die weiteren Themen interessieren, d.h. die DGL Systeme und Laplace Transformationen.
MfG
C. Schmidt |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 525
Registriert: 06-2001
| | Veröffentlicht am Freitag, den 28. März, 2003 - 13:16: | 
|
Hi Christian,
wärst du auch noch für einen kleinen "Anwendungsteil II" zur wiederholung und vertiefung zu haben bevor wir mit DGL systemen und Laplace durchstarten?
Oder lieber kein Ausflug in die Physik etc?
Gruß N.
|
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1077
Registriert: 02-2002
| | Veröffentlicht am Freitag, den 28. März, 2003 - 13:26: | 
|
Hi Niels
Ich wäre dafür direkt mit DGL Systemen anzufangen. DGLs höherer Ordnung zu lösen hab ich in den letzten Tagen schon gemacht, damit ichs nicht grad wieder verlern.
MfG
C. Schmidt |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 526
Registriert: 06-2001
| | Veröffentlicht am Freitag, den 28. März, 2003 - 17:02: | 
|
Hi Christian,
das habe ich mir schon gedacht. Ich habe dich hier im Forum nämlich beobachtet. Die DGL's aber waren ja auch nicht so schwer.
Frage:
wollen wir dann das neue Thema weiter unter gewöhnliche DGL's mit Teil V und folgende führen, oder lieber einen neuen Threat eröffnen?
Wenn du für einen neuen Threat bist, dann richte bitte einen mit dem Titel "Systeme lineare Differentialgleichungen" ein.
Ich warte auf deine Reaktion!
Gruß N.
ps: verlinke gegf. diesen Exkurs mit dem neuen
Threat als Anschlußexkurs!
|
    
Christian Schmidt (christian_s)

Senior Mitglied
Benutzername: christian_s
Nummer des Beitrags: 1080
Registriert: 02-2002
| | Veröffentlicht am Freitag, den 28. März, 2003 - 17:50: | 
|
Hi!
Ich hab mal einen neuen Thread geöffnet:
Systeme linearer Differentialgleichungen
MfG
C. Schmidt |
    
Niels (niels2)

Senior Mitglied
Benutzername: niels2
Nummer des Beitrags: 527
Registriert: 06-2001
| | Veröffentlicht am Freitag, den 28. März, 2003 - 19:01: | 
|
Hi Christian,
bevor wir zu den Systemen lin. Differentialgleichungen übergehen, noch ein Schlusswort zu Runge-Kutta:
Bei der Herleitung des Runge Kutta Verfahrens speziell mit der Gewichtung der einzelnen Steigungen gibt es gewisse Analogien zu der Keplerschen Fassregel, die wir aus der numerischen Integration kennen.
Es gibt aber auch noch mehr Runge Kutta Verfahren höherer Ordnungen und generell mehr Näherungsverfahren als wir hier besprochen haben. Aber alle anderen Runge-Kutta Verfahren weisen ebenfalls ähnlichkeiten zu numerischen Integrationsverfahren auf.(Simpsonregel, Newton-Cotes Formeln...)
Wenn man bedenkt, das es die Runge-Kutta Verfahren erst knapp 100 Jahre gibt, eine reife Leistung.
Nun aber genug gequasselt. Ich bedanke mich rechtherzlich beim "Auditorium" bei den Teilnehmern dieses "Mathematischen Seminars". Ich hoffe Sie konnten ein kleinen Einblick über die Lösungstechniken für gew. DGL's gewinnen, und die Einsicht mit nachhause mitnehmen, das DGL's in der Natur und Technik eine große Bedeutung haben. Es kann daher nicht Schaden ein bischen über das Lösen und die Natur von gew. DGL's zu wissen, daamit man wenn man auf sie im Altag stoßen sollte, mit ihnen fertig werden kann.
Ich hoffe wie gesagt, das dieser EXkurs etwas für sie, liebe Teilnehmer, etwas gebracht hat.
Sicher, was wir in diesen Exkurs besprochen haben haben wir nicht alles mathematische theoretisch exakt herleiten, beweisen, und begründen können; Aber ein Wenig Theorie haben wir ja auch besprochen.Die Praxis stand eindeutig hier im Vordergrund.Es soll genügen, wenn man jetzt nach dem Exkurs weis, wie man gewisse DGL's lösen kann.Die trockenen reine Mathematik dahinter soll erstmal verborgen bleiben.Lerning by Doing heißt das Motto, mit den hier gelehrt wird. Und wir gehen weiter im Thema, wenn sie mich nun zu den Systemen lin. gew. DGL's begleiten möchten....bitte herzlich willkommen!
mit freundlichen Grüßen
Niels |





