| Autor |
Beitrag |
    
Linda (ikoly)

Neues Mitglied
Benutzername: ikoly
Nummer des Beitrags: 1
Registriert: 02-2003
| | Veröffentlicht am Freitag, den 21. Februar, 2003 - 15:31: | 
|
Hallo, folgende Aufgaben sind mir schleierhaft.
1. Vergleichen Sie in einem gleichschnekligen Trapez mit Inkreis die Mittelparallele mit den Schenkeln.
( Ich hab das Trapez mal gezeichnet, aber wie bekomme ich da den Inkreis hin, oder soll man da gar nichts zeichnen ?, habe die Mittelparallele abgemessen, sie ist 0,5 cm länger als die Schenkel ) ????
2. Im gleichschnkligen Dreieck ABC sei D ein beliebiger Punkt der Basis AB . Beweisen Sie den Satz: Die Umkreise der Dreicke ADC und DBC haben einen gleich langen Radius.
( Ich habe das gezeichnet, aber das reicht ja nicht aus für den Beweis )
Vielleicht kann mir jemand helfen, bedanke mich !

|
    
mythos2002 (mythos2002)

Erfahrenes Mitglied
Benutzername: mythos2002
Nummer des Beitrags: 387
Registriert: 03-2002
| | Veröffentlicht am Samstag, den 22. Februar, 2003 - 00:04: | 
|
Hi,
das Trapez hat nur dann einen Inkreis, wenn der Schenkel b = d = (a/2) + (c/2) = (a+c)/2 ist.
Das sieht man, wenn man von allen Eckpunkten die Tangentenstücke an den Inkreis (sein Radius ist h/2) jeweils gleichsetzt (die Tangenten von einem Punkt an den Kreis sind gleich lang).
Die Mittenparallele ist immer m = (a+c)/2. Jetzt ist ersichtlich, dass die Mittenparallele gleich lang wie der Schenkel ist!
Gr
mYthos
|
    
Cooksen (cooksen)

Mitglied
Benutzername: cooksen
Nummer des Beitrags: 47
Registriert: 04-2002
| | Veröffentlicht am Montag, den 24. Februar, 2003 - 07:42: | 
|
Hallo Linda!
Schade, dass niemand den Beweis für deine 2. Aufgabe gefunden hat. Der hätte mich interessiert.
Gruß Cooksen |
    
Walter H. (mainziman)

Erfahrenes Mitglied
Benutzername: mainziman
Nummer des Beitrags: 402
Registriert: 05-2002
| | Veröffentlicht am Montag, den 24. Februar, 2003 - 08:38: | 
|
2.
basis AB = c
allgemein gilt:
R = abc/4A
weiters gilt:
A = b*c * sin(alpha)/2 bzw.
A = a*c * sin(beta)/2
AD = c1 = t*c mit 0 < t < 1 => a1 = sqrt(c1^2 + b^2 - 2c1b cos(alpha)) => A1 = bc1sin(alpha)/2
DB = c2 = (1-t)c => b2 = sqrt(c2^2 + a^2 - 2c2a cos(beta)) => A2 = ac2sin(beta)/2
R = abc/4A
a1bc1/[4(bc1sin(alpha)/2)] = ab2c2/[4(ac2sin(beta)/2)]
a1/(2sin(alpha)) = b2/(2sin(beta))
a1/sin(alpha) = b2/sin(beta)
a1/b2 = sin(alpha)/sin(beta)
sqrt(c1^2 + b^2 - 2c1b cos(alpha))/sqrt(c2^2 + a^2 - 2c2a cos(beta)) = sin(alpha)/sin(beta)
es gilt:
cos(alpha) = c1/b
cos(beta) = c2/a
sqrt(c1^2 + b^2 - 2c1^2)/sqrt(c2^2 + a^2 - 2c2^2) = sin(alpha)/sin(beta)
sqrt(b^2 - c1^2)/sqrt(a^2 - c2^2) = sin(alpha)/sin(beta)
sqrt(b^2 - t^2c^2)/sqrt(a^2 - (1-t)^2c^2) = sin(alpha)/sin(beta)
weiters gilt:
sin(alpha)/sin(beta) = a/b
sqrt(b^2 - t^2c^2)/sqrt(a^2 - (1-t)^2c^2) = a/b
(b^2 - t^2c^2)/(a^2 - (1-t)^2c^2) = a^2/b^2
b^2(b^2 - t^2c^2) = a^2(a^2 - (1-t)^2c^2)
b^4 - t^2b^2c^2 = a^4 - a^2c^2 + 2ta^2c^2 - t^2a^2c^2
Wer Lust hat, darf weiterrechnen.
Ein weiterer Weg wäre zu zeigen, daß beide Umkreismittelpunkte auf dem Kreis mit Mittelpunkt D liegen.
siehe dazu als Hinweis/Hilfe meine Facharbeit: Beweis und Herleitung der Euler'schen Geraden}
Gruß,
Walter
Mainzi Man,
ein Mainzelmännchen,
das gerne weiterhilft
oder auch verwirren kann *ggg*
|
    
Cooksen (cooksen)

Mitglied
Benutzername: cooksen
Nummer des Beitrags: 48
Registriert: 04-2002
| | Veröffentlicht am Mittwoch, den 26. Februar, 2003 - 18:04: | 
|
Hallo Mainzi Man!
Vielen Dank für Deine Rechnung und den Hinweis auf Deine Facharbeit.
Ich denke, der Beweis ist einfacher über die Kongruenz der Dreiecke DCM1 und DCM2 zu führen: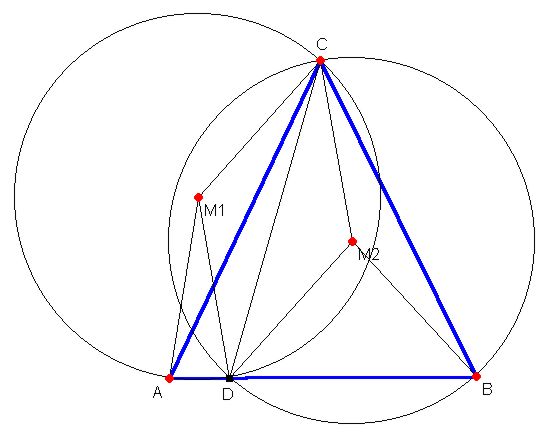
1. Beide Dreiecke sind gleichschenklig. Daher genügt es für die Kongruenz, wenn sie in einem Winkel und einer Seite übereinstimmen.
2. Der Winkel DM1C ist Mittelpunktswinkel über der Sehne DC und daher doppelt so groß wie der Peripheriewinkel DAC. Entsprechend ist der Winkel CM2D doppelt so groß wie der Winkel CBD. Die Winkel DAC und CBD sind aber die Basiswinkel des gleichschenkligen Dreiecks ABC und damit gleich groß. Folglich stimmen die beiden Winkel DM1C und CM2D überein.
3. Die Dreiecke haben die Seite DC gemeinsam.
Aus der Kongruenz der Dreiecke folgt die Gleichheit der Umkreisradien. q.e.d.
Gruß Cooksen |
    
Ringels (Ringels)

Neues Mitglied
Benutzername: Ringels
Nummer des Beitrags: 1
Registriert: 01-2008
| | Veröffentlicht am Freitag, den 04. Januar, 2008 - 09:35: | 
|
hallo
kann mir jemand sagen, wie ich R= abc/4A herleiten kann |
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 1901
Registriert: 03-2002
| | Veröffentlicht am Freitag, den 04. Januar, 2008 - 15:28: | 
|
Neue Frage -> neues Thema eröffnen! Nicht an einen 5 Jahre alten (!) Thread anhängen! So viel Aufwand sollte dir die Hilfe für dich schon noch wert sein!
Aus dem erweiterten Sinussatz
sin(alpha) = a/(2R); sin(beta) = b/(2R); sin(gamma) = c/(2R)
->
a = 2R sin(alpha)
und
der trigonometrischen Flächenformel
A = (bc/2) sin(alpha)
folgt durch Gleichsetzen von sin(alpha):
a/(2R) = 2A/(bc)
->
abc/(4R) = A
mY+ |
    
Mainziman (Mainziman)

Senior Mitglied
Benutzername: Mainziman
Nummer des Beitrags: 1529
Registriert: 05-2002
| | Veröffentlicht am Dienstag, den 10. Juli, 2012 - 20:59: | 
|
kann jemand den Link von meinem Post ändern?
Mainzi Man,
ein Mainzelmännchen-Export,
das gerne weiterhilft
oder auch verwirren kann *ggg*
|