| Autor |
Beitrag |
    
Anonym

| | Veröffentlicht am Samstag, den 20. März, 1999 - 17:03: | 
|
Der Graph der Funktion f(x) = ax²+bx+c geht durch die Punkte A(-2/1), B(-4/-2) und C(0/-4).
Gib die Funktion an und ihren Scheitel |
    
Adam Riese

| | Veröffentlicht am Sonntag, den 21. März, 1999 - 18:29: | 
|
Hi, Du mußt einfach die 3 bekannten (x/f(x))-Paare in die Funktions-Gleichung einsetzen und erhälst dann 3 Gleichungen mit den 3 Unbekannten a,b und c. Dieses Gleichungssystem löst Du auf und schon kennst Du f(x).
Ich fange mal an. Die Gleichungen kannst Du dann sicher selbst auflösen ... .
1) 1=a(-2)²+b(-2)+c => 1=4a-2b+c
2) -2=a(-4)²+b(-4)+c => -2=16a-4b+c
3) -4=a*0²+b*0+c => c=-4
Ausrechnen ergibt: a=-1, b=-9/2 und c=-4
Also gilt f(x)=-x²-9/2*x-4.
Jetzt machen wir eine quadratische Ergänzung, um den Scheitelpunkt zu erkennen:
f(x)=-(x+9/4)²+17/16
Das bedeutet, daß (-9/4 / 17/16) der Scheitelpunkt ist und das die Parabel nach unten geöffnet ist.
Der Graph von f(x) sieht also folgendermaßen aus:
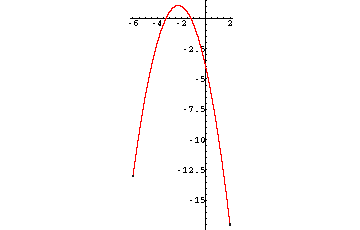
Hast Du es verstanden? Sonst frage ruhig nochmal nach!
Adam |
    
Anonym

| | Veröffentlicht am Mittwoch, den 31. März, 1999 - 20:28: | 
|
f(x)= 5x^3 - 3x^3 + 2 x
relative Extremstellen
Nulstellen
Graph
Wendepunkte |
    
Adam Riese

| | Veröffentlicht am Donnerstag, den 01. April, 1999 - 23:46: | 
|
Hi,
eine Frage, hast Du Dich vielleicht vertippt mit den 3x³ ??? Sind das 3x²? So wäre f(x) nämlich = 2x³+2x.
Bitte bestätige die Funktion nochmal bevor jemand die ganze Kette durchrechnet.
CU,
Adam |
    
Anonym

| | Veröffentlicht am Mittwoch, den 14. April, 1999 - 14:10: | 
|
Hi, kann mir jemand helfen ?
Ein Körper fliegt in einer Höhe von 25 m. Zum Zeitpunkt t = 0 sec mit einer Geschwindigkeit von v = 10 m / sec parallel zum Boden. Berechne seine Höhe über dem Erdboden zum Zeitpunkt t = 1 sec und t = 2 sec ! Der Fallweg beträgt: 4,9 x t² (in m). Wann erreicht der Körper den Boden ?
Welche strecke hätte sein Schatten dabei auf den Boden zurückgelegt ?
Beschreibe die Flugbahn des Körpers präzise ! Gib die Funktiongleichung an ! Begründe alle Aussagen.
Wer kann mir helfen. Noch heute, es ist wichtig. Und was ist der Fallweg in der parabel ?
Danke,
Christian |
    
Anonym

| | Veröffentlicht am Mittwoch, den 14. April, 1999 - 22:40: | 
|
Hi,
das ist ja Physik ... . Check mal in Mathefreie Zone > 16 Jahre die Links zu Physik. Da bekommst Du sicher optimale Hilfe.
Aber der Anfang:
Der Fallweg pro Sekunde beträft 4,9m => Nach 1 Sek. ist die Höhe 20,1m nach 2 Sek. 15,2 m.
Der Boden wird erreicht, wenn 4,9t²=25 gilt => t=Wurzel(25/4,9)= ...
....
.... |
    
Anonym

| | Veröffentlicht am Sonntag, den 09. Mai, 1999 - 14:28: | 
|
Hi ,kann mir irgendjemand bei diesen Aufgaben helfen, da ich null Durchblick habe?
f(x)=0,14285x2 + 7x + 6
f(x)=0,75x2+9x+6 |
    
Pi*Daumen

| | Veröffentlicht am Montag, den 10. Mai, 1999 - 23:18: | 
|
Hi, was ist denn die Aufgabenstellung ???
Zeichnen des Funktionsggraphen oder Nullstellenberechnung oder ... oder ... ??
Hier auf jedenfall mal die Skizzen der Funktionsgraphen:
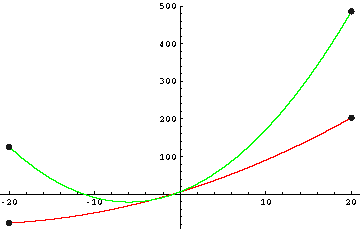 |
    
Susi

| | Veröffentlicht am Samstag, den 03. Juli, 1999 - 10:33: | 
|
Wer kann mir helfen?
Eine Funktion ist gegeben durch:
y=1/2 x+2(xEP)
a)zeichnen Sie den Graph dieser Funktion
b)berechnen Sie die Nullstelle dieser Funktion
c)untersuchen Sie,ob das Zahlenpaa(50;26) zu dieser Funktion gehört
d)-Zeichnen Sie die Gerade g2, die durch den Punkt A(0;-3)geht und parallel zu g; verläuft
-geben Sie die Gleichung der durch g2 dargestellten Funktion an |
    
Gerd

| | Veröffentlicht am Sonntag, den 04. Juli, 1999 - 19:45: | 
|
Hi Susi,
meinst Du y=(1/2)*x+2x ?
Gerd |
    
Roswitha

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 07. März, 2002 - 09:41: | 
|
Hallo!
Kann mir bitte vielleicht jemand helfen?
Kann ich die Gleichung y = x²-1
in die Scheitelpunktform bringen.
Danke.
Gruß Rosi |
    
Verena (Karabagh)

Neues Mitglied
Benutzername: Karabagh
Nummer des Beitrags: 1
Registriert: 11-2001
| | Veröffentlicht am Donnerstag, den 07. März, 2002 - 10:12: | 
|
Diese Gleichung y = x² - 1 ist bereits eine Form, von der man die Lage des Scheitelpunkts direkt ablesen kann. Es ist nämlich eine Normalparabel (x²), die um 1 nach links (auf der y-Achse) verschoben ist. Sie ist nach oben offen (+ x²). Mehr lässt sich nicht ablesen, was auch nicht erforderllich ist.
Gruß Verena |
    
Verena (Karabagh)

Neues Mitglied
Benutzername: Karabagh
Nummer des Beitrags: 2
Registriert: 11-2001
| | Veröffentlicht am Donnerstag, den 07. März, 2002 - 10:21: | 
|
Diese Gleichung y = x² - 1 ist bereits eine Form, von der man die Lage des Scheitelpunkts direkt ablesen kann. Es ist nämlich eine Normalparabel (x²), die um 1 nach links (auf der y-Achse) verschoben ist. Sie ist nach oben offen (+ x²). Mehr lässt sich nicht ablesen, was auch nicht erforderllich ist.
Gruß Verena |
    
Roswitha

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 07. März, 2002 - 11:27: | 
|
Danke Verena!
Gruß Roswitha |
|