| Autor |
Beitrag |
    
Niels

| | Veröffentlicht am Freitag, den 31. März, 2000 - 14:30: | 
|
Hi Reinhard,
da bin ich wieder.
Zu meiner Frage. Ich meine weder Sehnen, Sekanten noch Tangentensatz. Am besten gebe ich Dir eine genaue Konstruktionsbeschreibung der Überlegungsfigur.
1. Makiere auf einen Blatt Papier einen Punkt M.
2. Ziehe mit den Zirkel um M einen Kreis mit beliebigen Radius r.
3. Makiere 3 Punkte auf dem Kreis. Sie heißen A B und C.
4. Zeichne die Strecke AB, AC und BC. Es entsteht ein Dreieck, deren Seiten wir als AB=c, AC=b und BC=a bezeichnen.
5.Der Winkel in a Zwischen den Seiten bezeichnen wir als alfa, der in B und C jeweils als Beta und Gamma.
6.Konstriere in den Punkten A B C die Tangenten an den Kreis.
7. Trage an der Seite c in Punkt A den Sehnentangentenwinkel Epsilon an.
Beweise, das Epsilon genauso groß ist wie Gamma. Übertrage diesen Beweis (rechnerisch) auf die Übrigen Sehnentangentenwinkel.
Ist jetzt alles klar Reinhard?
Gruß
Niels |
    
reinhard

| | Veröffentlicht am Freitag, den 31. März, 2000 - 17:58: | 
|
Hallo Niels!
Es gibt da 2 Fälle: M ist im Dreieck drinnen, oder M ist eben nicht drinnen.
1. Fall: M ist im Dreieck:
Verbinde M mit A, M mit B und M mit C. Durch diese Verbindungslinien wird der Winkel a in die zwei Winkel a1 und a2, der Winkel b in b1 und b2 und der Winkel g in g1 und g2 geteilt.
Die drei Dreiecke AMC, CMB und BMA sind aber gleichschenkelig (mit dem Schenkel r), daraus folgt: a1=b2, b1=g2 und g1=a2.
In jedem Dreieck gilt: Die Summe der Innenwinkel ist 180°, so auch im Dreieck ABC:
a+b+g=180°
ich setze die Unterteilungen von oben ein:
a1+a2+b1+b2+g1+g2=180°
Nun kann ich aufgrund der 3 Gleichungen oben ersetzen:
a1+g1+g2+a1+g1+g2=180°
2a1+2(g1+g2)=180°
a1+g=90°
Der Winkel a1+e ist aber auch genau 90°, weil e an der Tangete anliegt, die zum Radius einen rechten Winkel einschließt.
Also ist a1=90°-e. Dieses eingesetzt:
90°-e+g=90°
e=g
2. Fall: M ist nicht im Kreis.
Hier kommt nur eine kleine Überlegung. Wenn du auch hier die Verbindungen von M zu den Punkten zeichnest, hast du in einem Winkel (hier in meiner Skizze ist das zufällig in b), die Unterteilung wie oben. In den anderen muß man folgenden Trick machen:
Ich nehme den Winkel MAB als a1, und MAC sehe ich als negativen Winkel an und nenne ihn (-a2). Dasselbe mache auch beim letzen Winkel.
Denn somit gilt wieder a=a1+(-a2)=a1-a2, und das stimmt ja, wenn du dir die Skizze ansiehst. Und da das Dreieck MCA genauso wie auch oben gleichschenkelig ist, gilt auch weiterhin (-a2)=(-g1).
Mit diesem kleinen Trick gilt alles wieder genauso wie im Fall, daß M im Dreieck ist - und somit geht dieser 2.Fall in den 1.Fall über.
Diesen Beweis kannst du leicht auf die anderen Sehnentangentenwinkel übertragen, indem du einfach die Punkte umbenennst und dieselbe Rechnung nocheinmal darüberlaufen läßt.
Reinhard |
    
Niels

| | Veröffentlicht am Freitag, den 31. März, 2000 - 19:37: | 
|
Hi Reinhard,
Erstmal Danke für deine Bemühung mir disen Bweis näher zu bringen.
Aber, köntest du mir nochmal deine Skizze schicken? Ich glaube, das ich dann besser deine Überlegungen nachvollziehen könnte.
Ach so, nochmal zum Benutzerkonto,würde jeder eigentlich die neuen Nacchten aus seiner gewälten kategorie erhalten, wenn er ein Benutzerkonto besäße, oder wird dieses Privileg nur den eingefleischten Zahlreich Moderatoren zum teil?
Vielen Dank Reinhard!!!
Gruß
Niels |
    
reinhard

| | Veröffentlicht am Freitag, den 31. März, 2000 - 19:57: | 
|
Hi Niels!
Also hier sind die zwei Skizzen.
Zuerst die für Fall 1:
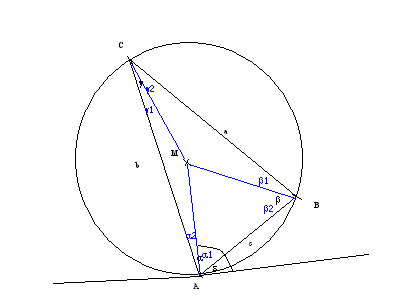
und hier für Fall 2:
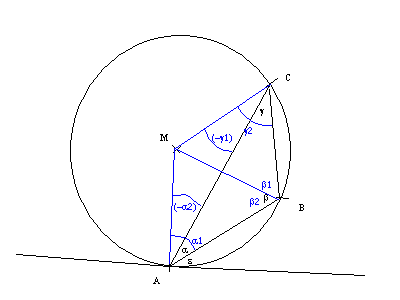
Nein, das mit dem Benutzerkonto kann jeder haben. Im linken Frame unter "Features/Benutzerkonto" kannst du dir auch eines einrichten. Wenn man vor hat, hier öfter ein paar Nachrichten zu beantworten, zahlt sich das Konto definitiv aus.
Reinhard |
    
Niels

| | Veröffentlicht am Freitag, den 31. März, 2000 - 20:02: | 
|
Hallo Reinhard!
Danke dir für die Skizzen.
Gruß
Niels |
    
reinhard

| | Veröffentlicht am Freitag, den 31. März, 2000 - 20:06: | 
|
Hallo Niels!
Tut mir leid, daß ich das geschrieben habe, aber ich wollte dir eben noch einen Vorteil von Benutzerkonten demonstrieren. Wenn du ein Konto mit dem Benutzernamen "Niels" gehabt hättest, wäre es mir nicht möglich gewesen, diese Nachricht zu schicken, weil ich dann dein Passwort nicht gewußt hätte. Bei einem Benutzerkonto ist der Benutzername ganz für dich alleine reserviert, und es kann keine Mißverständnisse geben, wenn irgendein anderer Niels auch unter dem Namen "Niels" Nachrichten hier verschickt.
Reinhard |
    
Niels

| | Veröffentlicht am Freitag, den 31. März, 2000 - 20:50: | 
|
Hi Reinhard,
danke nochmals für die Skizzen,
ich habe jetzt alles begriffen.
Ich habe mir das mit den Benutzerkonto auf der linken Seite gründlich durchgelesen und mir ist im letzten Satz etwas aufgefallen, ich kann mich dort sofort registrieren lassen (Auch wenn ich noch kein Benutzerkonto besitze).Was hat das mit der "Sofort Registrierung" auf sich und Was würdest du mir emfehlen? Benutzerkonto oder diese Registrierung?
Danke im Vorraus Reinhard!!
Gruß
Niels |
    
reinhard

| | Veröffentlicht am Freitag, den 31. März, 2000 - 21:18: | 
|
Das mit dem "sofort Registrieren" gilt gerade dann, wenn du noch kein benutzerkonto hast. Diese Registrierung dient zur erhebung wichtiger Daten für die Erstellung deines Benutzerkontos (gewünschter Benutzername, Passwort, e-mailadresse an die dann die Nachrichten geschickt werden, etc)
Also auf den Button "Sofort Registrierung" drücken und dann den Anweisungen folgen. Ist eigentlich alles ziemlich selbserklärend.
Reinhard |
    
Niels

| | Veröffentlicht am Freitag, den 14. April, 2000 - 07:57: | 
|
Hi Reinhard,
sind die 2 Fälle beim Sehnentangentenwinkel wirklich so wichtig? oder könnte man das ganze Unternehmen auch über ein Gleichungssystem mit 3 Variablen fahren?
Außerdem wäre ich an der Heerleitung des Sekantensatzes und des Tangentensatzes (Sekantentangentensatzes) interressiert.
der Sehnensatz war mit den Ähnlichkeitssätzen zimlich einfach herleitbar. Nur bei den anderen beiden Sätzen habe ich Probleme ähnliche Dreiecke zu finden.
könntest du mir helfen?
Gruß
Niels |
    
Niels

| | Veröffentlicht am Freitag, den 14. April, 2000 - 09:16: | 
|
Hi Reinhard,
sind die 2 Fälle beim Sehnentangentenwinkel so wichtig, oder könnte man auch per Gleichungssystem den Beweis erbringen?
Zusätzlich würde mich jetzt der Beweis des Sekantensatzes und Tangentensatzes per ähnliche Dreiecke interressieren. Ich habe nämlich Schwierigkeiten solche Dreiecke zu finden.
kannst du mir bei der Herleitung helfen?
Danke schon mal!!
Gruß
Niels |
    
reinhard

| | Veröffentlicht am Freitag, den 14. April, 2000 - 10:39: | 
|
Hallo Niels!
Diese Unterscheidung in 2 Fälle ist der Form halber notwendig. Denn wenn ich nur den einen Fall bearbeite, könnte der berechtigte Einwand kommen: "Was aber, wenn M nicht im Dreieck liegt, so wie es die ganze Zeit gezeichnet wurde?" Und um eben diesem Vorzubeugen, zeigt der 2. Fall, wie man dann die Winkel bezeichnen muß, damit die Rechnung aus dem 1. Fall trotzdem stimmt.
Der Beweis an und für sich besteht ja nur aus der Umformung der Gleichung. Die zwei Fälle dienten nur zur Veranschaulichung, wie die Winkel benannt werden sollen.
Und hier der Beweis für den Tangentensekantensatz:
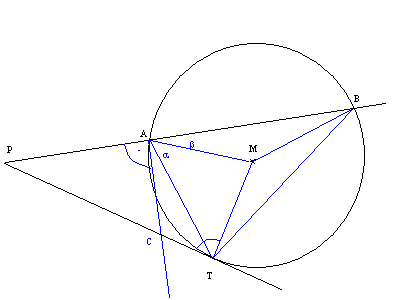
Mit schwar wieder die Voraussetzungen:
Zieht man von einem Punkt außerhalb des Kreises eine Sekante und eine Tangente, so sei die Strecke PA=a und PB=b und PT=x, dann gilt: x²=ab.
Wir zeichnen wieder Hilfslinien: Wir verbinden die Punkte A-B-T zu einem Dreieck und zeichnen die Strecken MA, MB und MT ein. Weiters wird in A die Normale auf PA eingezeichnet. Wo sich diese Normale mit PT schneidet sei der Punkt C.
Ich Vermute, daß die Dreiecke PAT und PTB ähnlich sind. und es gilt: PA:PT=PT:PB. die oben definierten bezeichnungen eingesetzt:
a/x=x/b
a*b=x*x
und damit wäre der satz bewiesen. Es bleibt nur noch zu zeigen,daß diese beiden Dreiecke wirklch ähnlich sind:
Beiden gemein ist der Winkel APT. Außerdem werde ich zeigen, daß der Winkel PAT gleich groß ist wie der Winkel PTB. Somit sind 2 Winkel ident und die Dreiecke sind ähnlich.
Ich unterteile den Winkel PAT in die Winkel PAC+CAT. PAC ist laut definition für die Konstruktion des Punkts C ein rechter Winkel. Also ist PAT=90°+CAT.
Den Winkel PTB kann ich auch in PTM+MTB unterteilen. auch hier ist PTM ein rechter Winkel, weil T ein Tangentialpunkt ist.
Also ist PTB=90°+MTB.
Nun genügt es zu zeigen, daß CAT=MTB ist, denn dann sind auch PAT=PTB.
Wie du aus der Skizze bemerkst, habe ich den Winkel TAM a und den Winkel MAB b genannt.
Der Winkel CAT ist gleich 90°-a-b. Dies merken wir uns.
Wenn der TAM=a ist,dann ist auch ATM=a, weil das Dreieck ATM gleichschenkelig ist. Und damit ist der Winkel AMT=180-2a.
Ebenso gilt, daß der Winkel ABM=b, weil BAM=b und auch dieses Dreieck gleichschenkelig ist. Und so ist auch der Winkel AMB=180-2b.
Die Winkel TMB+BMA+AMT ergeben einen vollen Kreis.
Also 360=TMB+BMA+AMT
TMB=360-BMA-AMT.
BMA ist aber 180-2b und AMT ist 180-2a
TMB=360-(180-2b)-(180-2a)=2b+2a
Das Dreieck TMB ist nun aber auch gleichschenkelig und der Winkel MTB ist (180-TMB)/2.
also:
MTB=(180-(2b+2a))/2=90-a-b
Nun haben wir zuvor festgehalten, daß CAT=90-a-b. Und nun haben wir berechnet, daß auch MTB=90-a-b.
Damit sind die Winkel CAT und MTB gleich groß.
Das war der letzte Schritt, um zu zeigen, daß die zwei Dreiecke PAT und PTB ähnlih sind, und somit gilt auch die Behauptung x²=ab.
Reinhard |
    
Niels

| | Veröffentlicht am Freitag, den 14. April, 2000 - 14:28: | 
|
Hi Reinhard,
nochmals danke für die Herleitung des Sekantentangentensatzes.
Ich hab da aber nochmal zwei Frage:
1. Frage: (zum Sehnentangentenwinkel)
Ist das mit den Zwei Fällen den nicht irrelewant weil im Gleichungssystem nur mit winkel gearbeitet werden würde (Innenwinkelsatz im dreieck; Komplementärwinkeln)? Also würden Strecken und der Mittelpunkt gar nicht erwähnt werden.
2. Frage (zum Sehnensatz):
Wie ich schon gesagt habe, habe ich den Satz mit hilfe von ähnlichen Dreiecken hergeleitet. Du meinst, man könnte ihn auch per Cosinussatz herleiten. Wie macht man das?
Danke nochmal im Vorraus!!
Gruß
Niels |
    
reinhard (Gismo)

| | Veröffentlicht am Samstag, den 15. April, 2000 - 13:44: | 
|
Hallo Niels!
Zu Frage 1:
Wie schon gesagt: Der Beweis kommt ohne die Fallunterscheidung aus, nur zur Verdeutlichung und zum besseren Verständniss habe ich die BENENNUNG der Winkel für die zwei Fälle, daß M im Dreieck und daß M nicht im Dreieck ist, angeführt. Ich habe dies mit dem Grundsatz "Wenn es nichts hilft, so schadet es auch nichts" gerechnet.
Zu Frage 2:
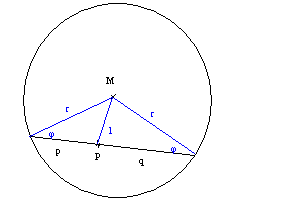
Voraussetzung (schwarz gezeichnet): Wird in einem Kreis durch einen festen Punkt P eine Sehne gezeichnet, so ist das Produkt der Abschnitte konstant.
Zeichne Hilfslinien: Verbindung von M zu P und von M zu den beiden Schnittpunkten der Sehne mit dem Kreis. Zur Benennung: die Sehne wird durch den Punkt P in die Teilstücke p und q geteilt. Der Abstand des Punktes vom Kreismittelpunkt ist l und r ist der kreisradius.
Da das Dreieck, das aus Sehne und den zwei Radien gebildet wird, gleichschenkelig ist, sind auch die Winkel an den Enden der Sehne gleich. Ich nenne diesen Winkel j.
Die Strecke l trennt das große Dreieck in zwei kleine, für die man den Cosinussatz anwenden kann:
l²=r²+p²-2rp*cos(j)
l²=r²+q²-2rq*cos(j)
diese beiden Gleichungen nach cos(j) aufgelöst und gleichgesetzt:
(r²+p²-l²)/2rp=(r²+q²-l²)/2rq
(r²+p²-l²)q=(r²+q²-l²)p
q(r²-l²)+p²q = p(r²-l²)+q²p
q(r²-l²)-p(r²-l²) = q²p-qp²
(q-p)(r²-l²) = qp(q-p)
Hier nehme ich an, q-p ist ungleich 0. Für den Fall, daß q-p doch 0 ist, werde ich anschließend eine Fallunterscheidung machen
r²-l²= qp
Da r und l nur vom Kreis und dem Punkt P abhängen, und nicht davon, wie die Sehne durchgelegt wird, ist r²-l² eine Konstante. Und für jede beliebige Sehne ist das Produkt ihrer Abschnitte gleich dieser Konstante.
Nun der Fall, daß q-p=0 (sonst hätten wir vorher nicht durch q-p dividieren dürfen). Das heißt, q=p. Die Länge l wäre dann die Schwerlinie des gleichschenkeligen Dreiecks, also auch gleichzeitig die Höhe (in einem gleichschenkeligen Dreieck fallen Höhe, Winkelhalbierende und Schwerlinie zusammen). Und das heißt, daß l auf die Sehne normal stehen würde. Somit könne man den pythagoras anwenden:
p²=r²-l²
q²=r²-l²
p²q²=(r²-l²)(r²-l²)=(r²-l²)²
pq=(r²-l²)
Das Produkt der Abschnitte ergibt also auch dann den konstanten Wert, wenn q-p=0.
Reinhard |
    
Niels

| | Veröffentlicht am Sonntag, den 16. April, 2000 - 18:42: | 
|
Hi Reinhard,
Danke nochmals für die (bisherigen) Herleitungen.
Aber mein Wissensdurst ist leider immer noch nicht gestilt.
1.Frage:
Der Sehnensatz beginnt doch volgendermaßen:
Schneiden sich 2 Sehnen in einem Punkt P innerhalb des Kreises....
In deiner Skizze sehe ich jedoch nur eine Sehne, wo ist die andere Sehne?
Oder ist das egal, weil du bewiesen hast, das die Produckte der Sehnenabschnitte konstant ist?
2. Frage: beschreibt der Sekantentangentensatz und der Tangentensatz den gleichen Sachverhalt?
In meinen Büchern steht immer nur Tangentensatz, aber ich glaube das andere ist nur eine andere überschrift für die gleiche Sache.
3.Frage:
Wie lautet die Diffinition einer Normalen am (im) Kreis?
Was eine Passante;Sekante;Sehne und Tangente ist weiß ich, nur bei der Normale habe ich Zuordnungsschwirigkeiten.
Und Nun habe ich noch eine Bitte an dich:
wie leite ich mit Ähnlichen Dreiecken den Sekantensatz her?
Ich wäre Dir für die Bearbeitung dieser Fragen sehr Dankbar und werde (versuchen) dich nicht mehr mit diesen (unangenehmen)Thema belästigen.
Gruß
Niels
ps: Deinen Grundsatz muß ich mir merken!!! |
    
reinhard (Gismo)

| | Veröffentlicht am Sonntag, den 16. April, 2000 - 21:48: | 
|
Hallo Niels!
1.
Ja, wie du selber schon festgestellt hast, ist es egal. Denn wenn für eine belibige Sehne mit den Abschnitten p und q gilt: pq=r²-l², und auch für eine andere mit den Abschnitten p' und q' gilt: p'q'=r²-l², dann folgt doch, daß für zwei beliebige Sehnen gilt: pq=p'q'.
2.
Auch hier hast du recht. Ist ersteinmal der Tangentensekantensatz bewiesen, dann kann man daraus den Sekantensatz folgern.
3.
Ich bin nicht sicher, wie die Normale an einen Kreis definiert ist, aber ich bin mir ziemlich sicher, daß eine Normale an einen Kreis genau die Normale auf die Tangente an jenem Punkt am Kreis ist. So ist nämlich ganz allgemein die Normale an einer Kurve definiert.
Tangenten an den Kreis stehen immer normal auf die Strecke vom Tangentialpunkt zum Mittelpunkt. Das heißt, eine Normale an einen Kreis geht immer durch den Kreismittelpunkt und jeder Radius ist eine Normale an den Kreis.
Wenn es heißt, von einem Punkt aus soll eine Normale an einen Kreis gelegt werden, dann heißt das, von dem Punkt aus soll eine Gerade durch den Kreismittelpunkt gelegt werden.
Ich hoffe, du verstehst, was ich meine.
Was den Beweis des Sekantensatzes betrifft, da müßte ich erst ein wehnig herumtüfteln, aber heute ist es schon etwas spät. Ich hoffe aber, dir morgen den Beweis schicken zu können.
Reinhard
PS:
Das möchte ich überlesen haben, daß du das finden von geometrischen Beweisen als unangenehmes Thema bezeichnest. Das ist nämlich fast soetwas wie mein Lieblingsgebiet. Das Geometrie-Beispiel war auch bei der IMO '97 das einzige, wo ich die volle Punktezahl erreicht habe und somit eine "Honorible Mention" erziehlt habe. |
    
Niels

| | Veröffentlicht am Montag, den 17. April, 2000 - 08:13: | 
|
Hi Reinhard,
Mein Vorschlag zur Normalen wäre gewesen:
Die Normale ist eine Sekante durch den Kreismittelpunkt M.
Ist das korrekt?
Tut mir leid mit meiner Aussage zum Schluß.Nur Geometrie ist normalerweise nicht mein Spezialgebiet. Ich rechne lieber als zu zeichnen.
Aber zum Glück kann ich mich ja (hoffentlich) bei Problemen in Geometrie auf deine kompetente Hilfe verlassen!
Was für ein Mathematikwettbewerb war IMO 97?
und was ist eine "Honorible Mention"?
Danke!!
Gruß
Niels |
    
reinhard (Gismo)

| | Veröffentlicht am Montag, den 17. April, 2000 - 18:41: | 
|
Hallo Niels!
Dein Vorschlag zur Normalen ist genau das, was auch ich vermutet habe, nur etwas kürzer gesagt.
Hier erstmal der Beweis. Ist eigentlich ziemlich einfach. Hätte ich das gewußt, wäre der Beweis gestern auch noch leich gegangen:

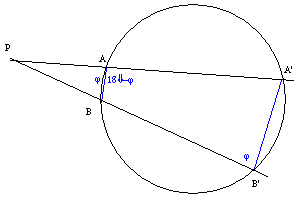
PA=a, PA'=a', PB=b, PB'=b'. Der Satz sagt:
aa'=bb'.
Wir zeigen wieder, daß die Dreiecke PAB und PA'B' ähnlich sind.
Einen gemeinsamen Winkel haben sie ja (nämlich APB).
Wenn man A und B verbindet, und A' und B' auch, dann erhält man ein sogenanntes Sehenviereck, und solche Sehnenvierecke haben die Eigenschaft, daß die Summe der gegenüberliegenden Winkel 180° ist. Wenn der Winkel PB'A' j ist, dann ist der Winkel BAA' genau 180-j (eben wegen dem Sehnenviereck). Und daraus folgt, daß der Winkel PAB wieder j ist, weil er der Nebenwinkel von BAA' ist.
Zwei gleiche Winkel genügen, daß zwei Dreiecke ähnlich sind:
a:b=b':a'
aa'=bb'
fertig.
Die IMO ist die Internationale Mathematik Olympiade, die jedes Jahr stattfindet, und an der aus ca 80 Länder der ganzen Welt je 6 Schüler teilnehmen (Schüler heißt unter 20 Jahren und keine Universität oder ähnliches besuchen). 1997 was sie in Argentinien in Mar Del Plata, ja und da durfte ich Österreich vertreten. Die Aufgaben sind natürlich dementsprechend schwierig, und wenn jemand ein Beispiel vollkommen richtig lösen kann, aber keine Medaille bekommt, dann wird ihm zumindest eine spezielle Urkunde, eine sogenannte "honorible Mention" (zu Deutsch: ehrenhafte Erwähnung) überreicht.
Wenn ich mich recht erinnere, bist du ja noch Schüler. Frag mal bei deinem Mathematiklehrer nach. Irgendwo in deiner Umgebung ist sicher ein Kurs für die Mathematik Olympiade. Da solltest du auch mal mitmachen. Ich habe auch nur aus Interesse dort angefangen, weil man da einfach mehr lernt, als im regulären Unterricht, naja, und dann habe ich aufeinmal einen schönen 2-Wochen-Urlaub in Argentinien gehabt (die ersten 2 Tage mußten wir rechnen, die restlichen 1 1/2 Wochen wurden die Arbeiten dann verbessert).
Reinhard |
    
Niels

| | Veröffentlicht am Montag, den 17. April, 2000 - 21:24: | 
|
Hi Reinhard,
hälst du mich etwa für befähigt an solchen Wettbewerb teil zu nehmen?
Danke erstmal für die Beweise, nur noch eines, die letzte Grafik ist nicht angekommen.
Könntest du noch die Letzte Skizze schicken?
Das wäre echt toll, danke Reinhard!!
Gruß
Niels |
    
franz

| | Veröffentlicht am Dienstag, den 18. April, 2000 - 07:35: | 
|
Hallo Reinhard, wieviele Bewerber kommen auf einen Teilnehmer der IMO? Gruß F. |
    
reinhard (Gismo)

| | Veröffentlicht am Dienstag, den 18. April, 2000 - 14:43: | 
|
Hier erstmal die Skizze:
Warum solltest du nicht "fähig" sein, an der Mathematik-Olympiade teilzunehmen? Ich denke aber, du hast auf jeden Fall die Interesse! Man besucht ein Jahr lang einen Kurs (bei mir waren das 1,5 Std/Woche), in dem man mathematische Methoden und Beweise, über den Schulstoff hinaus, lernt. Daß es dann gegen Ende des Jahres einen Bewerb gibt, sollte nicht der hauptsächliche Grund für eine Teilnahme sein.
In Linz war 1997 so ein Kurs, und da waren ca 15 Schüler. Mitte 2. Semester war dann ein Bewerb. Die besten 3 stiegen zum Gebietswetbewerb auf (ich war erster).
Beim Gebietswetbewerb kannen sämtliche Kursgewinner aus Oberösterreich, Salzburg und Tirol (Ö wird in 3 Gebiete aufgeteilt) zusammen (es werden wohl so 40 bis 60 Teilnehmer gewesen sein). Hier die besten 10 (ich war zweiter) kamen zum Staatsbewerb.
Der staatsbewerb beinhaltete wieder einen extra-Kurs als Spezialvorbereitung für die IMO und dann einen Bewerb. Und von diesen 29 (einer war damals zuvor krank geworden) fuhren die besten 6 (ich war fünfter) zur IMO.
Ich kann mir gut vorstellen, daß in Deutschland noch ein paar mehr Bewerbe sind (oder jeweils mehr Teilnehmer), weil Dt einfach entsprechend größer ist, trotzdem aber auch nur 6 Kandidaten zur IMO dürfen.
Es kommen also eher viele Bewerber auf einen Teilnehmer. Man braucht nicht nur mathematisches Wissen, sondern auch noch eine Portion Glück, daß genau Beispiele kommen, die einem liegen.
Wie schon gesagt, am interessanteren ist der Kurz zuvor. Die Bewerbe sind dann das Tüpfchelchen auf das i.
Reinhard |
    
Jan (Jan)

| | Veröffentlicht am Montag, den 24. April, 2000 - 20:56: | 
|
Bitte um Hilfe!
Ein Rechteck mit den Seiten a= 2cm, b= 6cm ist zeichnerisch in ein Quadrat zu verwandeln:
a) nach dem Tangentensekantensatz
b) nach dem Sehnensatz
Danke im voraus Jan |
    
Niels

| | Veröffentlicht am Dienstag, den 25. April, 2000 - 08:01: | 
|
Hi Jan,
zum Sehnensatz:
Zeichne in einem Kreis mit der Länge a+bcm.(hier 8cm). Der Teilpunkt P teilt diese Strecke in einen a und b Abschnitt. Verbinde P mit dem Mittelpunkt M des Kreises.Errichte an der Strecke MP in Punkt P das Lot als 2-te Sehne. das Quadrat aus den Abschnitten der 2-ten Sehne ist das gesuchte Quadrat.
Gruß
Niels |
    
Niels

| | Veröffentlicht am Dienstag, den 25. April, 2000 - 09:28: | 
|
Hi Jan,
ich bin es nochmal.
Zum Tangentensekantensatz:
Zeichne eine Strecke AB mit der Länge a+bcm (Also 8 cm).Der Punkt P teilt diese Strecke in den a und b Abschnitt. Halbiere die Strecke PB=b=6cm.
Ziehe um den Mittelpunkt M dieser Strecke ein Kreis mit Radius r=PM=MB=3cm. Konstruiere von A aus die Tangente t an den Kreis. Das Quadrat über den tangentenabchnitt ist das gesuchte Quadrat.
Gruß
Niels |
    
franz

| | Veröffentlicht am Dienstag, den 25. April, 2000 - 18:33: | 
|
Auf einer Geraden g Punkte S, D (SD=a) und C (SC=b) zeichnen, auf der Mittelsenkrechten zu CD ein Punkt M. An die Peripherie des Kreises um M (r=MC) von S aus eine Tangente (zum Beispiel durch Schnitt mit dem Thaleskreis über SC) an den Punkt A. Rechteck a=SD, b=SC -> Quadrat c=SA (Sekantentangentensatz).
Durch AB=b Mittelsenkechte, darauf beliebig M, Kreis um M (r=MA). Nach innen S (AS=a), Senkrechte zu MS, schneidet Kreis in C. a,b -> c=SC, Sehnensatz. F. |
    
Niels

| | Veröffentlicht am Mittwoch, den 26. April, 2000 - 17:00: | 
|
Hallo Reinhard,
Ich habe mich nochmal um den "Randwinkelsatz" gekümmert.
Wir haben ihn heute in der Schule nochmals mit hilfe eines Gleichungssystems hergeleitet.
Für unseren Mathelehrer ist der Randwinkel der Sehnentangentenwinkel.Dementsprechent ist er formuliert:
Randwinkelsatz:
Der Rantwinkel ist genauso groß wie der gegenüberliegende Innenwinkel.
wir brauchen ihn für eine weitere Herleitung des Sinussatzes.
Ist mir zwar (noch) schleierhaft wie beide Sätze zusammenhängen, aber warten wir es ab.
Gruß
Niels |
    
reinhard (Gismo)

| | Veröffentlicht am Mittwoch, den 26. April, 2000 - 20:42: | 
|
Hallo Niels!
Entschuldige meine Ungeduld, aber bei dem Hinweis, den Sinussatz mit dem Randwinkelsatz herzuleiten, mußte ich dies einfach tun und nun mein Ergebnis kundtun (ist nämlich genial simpel). Ich hoffe, ich verderbe dir damit nicht die Vorfreude auf den Unterricht.
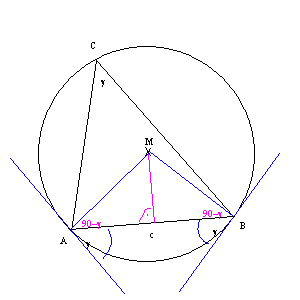
Wie mit dem Randwinkelsatz bewiesen, ist der Randwinkel an A und an B gleich dem Winkel g.
Mit grün nun die weiteren Überlegungen: wir zeichnen im gleichschenkeligen Dreieck ABM mit der Schenkellänge r die Höhe auf c ein. Bei Gleichschenkeligen Dreiecken wir die Basis von der Höhe halbiert.
In den zwei Teildreiecken ist der Winkel MAB=MBA=90°-g. In rechtwinkeligen Dreiecken gilt:
cos(j)=Ankathete/Hypothenuse
Für unsere Teildreiecke:
cos(90°-g)=(c/2)/r=c/2r
Da cos und sin bis auf die Phasenverschiedenheit ident sind, gilt:
cos(90°-g)=sin(g)=c/2r
2r=c/sin(g)
Dasselbe Spiel kann man nun auch an der Seite a spielen und man wird zum Ergebnis 2r=a/sin(a) kommen. Und haarscharf dieselbe Rechnung an der Seite b angewandt ergibt 2r=b/sin(b).
In dem Dreieck ist r eine Konstante, weshalb gilt:
2r=a/sin(a)=b/sin(b)=c/sin(g)
Und das ist die Herleitung (oder der Beweis) des Sinussatzes.
Ich muß sagen, euer Lehrer macht einen Interessanten Unterricht. Bei uns wurde der Sinussatz an die Tafel geschrieben, 3 mal rot unterstrichen und weiter wurde nichts gesagt, weil er ja ohnehin leicht zu merken ist und an der Richtigkeit dieses Satzes niemand zu zweifeln wagte, weshalb - so der Lehrer - auch kein Beweis nötig wäre.
Reinhard |
    
Niels

| | Veröffentlicht am Mittwoch, den 26. April, 2000 - 21:31: | 
|
Hi Reinhard,
Der unterricht ist hoch interressant. Was meinst du warum ich so ein interresse an der Mathematik habe! Ich habe ihn schon seid 4 Jahren und bedaure es schon, das ich ihn nur noch 1/4 Schuljahr haben werde.Er ist (war) mein Lieblingslehrer.
War Dir diese Beweisführung noch unbekannt?
Mal sehen, wenn wieder was interressantes kommt werde ich dich informieren.
(Fals du daran interresse hast)
Gruß
Niels |
    
sandra (Sandramaus)

| | Veröffentlicht am Mittwoch, den 05. Juli, 2000 - 18:51: | 
|
Gegeben sind ein Kreis k (M;r) mit r = 6 cm und ein Punkt P mit Strecke PM = 10 cm. ZEichne die beiden Tangenten von dem Punkt P an den Kreis k und berechne die Länge der Tangentenabschnitte.
Bitte um schnellstmögliche Nachricht !!!!!
Sehr wichtig !!!!!
Dankeschön. |
    
Kai

| | Veröffentlicht am Donnerstag, den 06. Juli, 2000 - 21:44: | 
|
Sollst Du die Länge ausmessen oder mit Pythagoras und so ausrechnen?
Kai |
    
Fern

| | Veröffentlicht am Freitag, den 07. Juli, 2000 - 08:44: | 
|
Hallo Sandra,
Länge des Tamngentenabschnittes=
Wurzel((PM)²-r²)= Wurzel(100-36) = 8 cm |
    
horst

| | Veröffentlicht am Dienstag, den 29. Mai, 2001 - 07:36: | 
|
hallo ich bin horst ihr ••••••••••• |
    
schulprobleme

| | Veröffentlicht am Dienstag, den 29. Mai, 2001 - 07:42: | 
|
hallo ihr !könnt ihr uns sagen was ein tangentensekanten - satz ist??????
bitte ganz schnell antworten!!DANKE! |
    
J

| | Veröffentlicht am Dienstag, den 29. Mai, 2001 - 08:11: | 
|
Zeichne einen Kreis K und einen Punkt P ausßerhalb des Kreises!
Zeichne von P aus eine Tangente an den Kreis K! Nenne den Berührpunkt B!
Zeichne von P aus irgendeine Sekante durch den Kreis K! Nenne die Schnittpunkte X und Y!
Der Satz sagt, dass gilt:
|PB|² = |PX|*|PY|
Dabei bezeichnet |PB| die Länge der Strecke PB.
Gruß J |
    
Kellan

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 17. April, 2008 - 19:33: | 
|
Ich brauche dringend und schnell eine Lösung:
Beweise: Wenn sich bei einem Kreis eine Tangente und eine Sekante im Punkt S schneiden,dann ist das Produkt der Längen der beiden Sekantenabschnitte SC un SD gleich dem Quadrat der Längedes Tangentenabschnittes. (Sekanten-Tangenten-Satz) |
|